
LAMA is now coded in RECYCLE, so we are ready to begin our simulations in CardStock with both random and AI players. As before, to gather statistics for this post, we ran 100 games with all random players, 100 games with one AI and the rest random players, and 100 games with all AI players.
In an excellent overview video, W. Eric Martin discusses why he believes LAMA is an excellent candidate for the 2019 Spiel Des Jahres. He talks about how LAMA feels very different in two-player games than in four-player games, or six-player games. To help us get a sense of why, we ran our LAMA simulations for 2, 3, 4, 5, and 6 players.
The full game of LAMA takes place over multiple rounds, ending when one player passes 40 points. However, in this first post I’ll be simulating only a single round, to get a feel for how the game is played, and then compare these results to the full game in a later post.
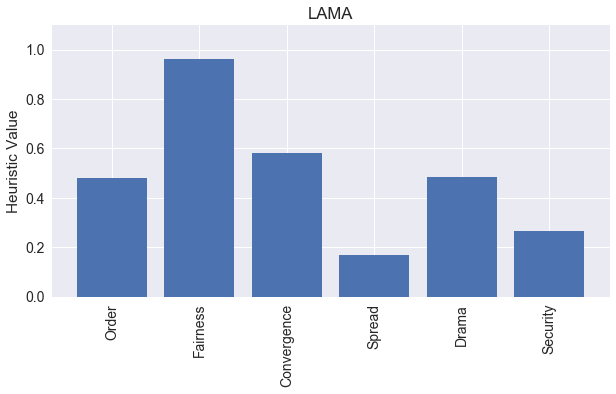
Let’s see how it scores on our heuristics of Order, Fairness, Convergence, Spread, Drama, and Security.
(See this previous post for a review of the heuristics I’ll be discussing.)
Order = 0.48
First, we’ll see how the AI players fare against chaos. Order captures the ability of the AI player to win when pitted against random players.
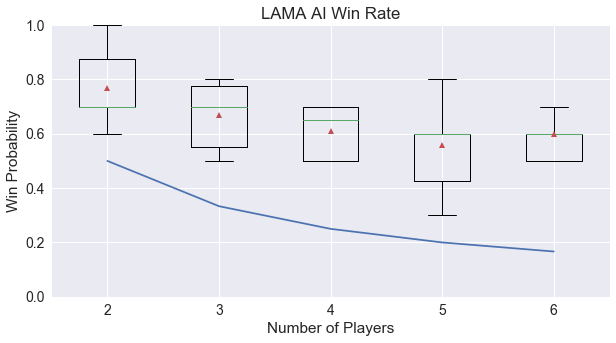
We can see that in LAMA, the AI players perform quite well! Better than Agram and Stealing Bundles, but not as high as Ninety-Eight. I suspect that the random players are folding and drawing more often when they should be playing their cards to the discard pile.
Fairness = 0.96
Next, we’ll examine if the game is fair, measured by determining if the first player wins more or less as expected. The following figure shows the average win rate of the first player as the number of players in the game varies.
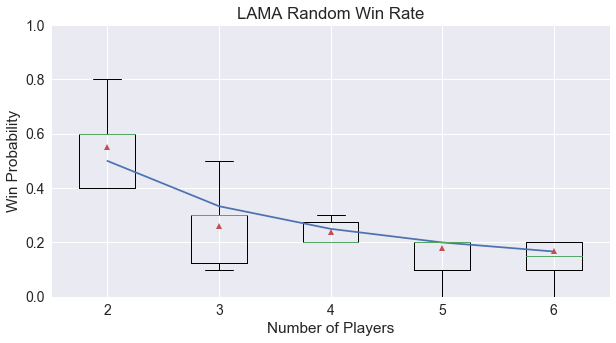
LAMA is a very fair game when looking at an individual round, and this appears to be the case no matter the number of players. This is good news for the full game, since the starting player for the next round can be chosen in whatever manner is easiest to remember, instead of needing to balance out any individual-round bias.
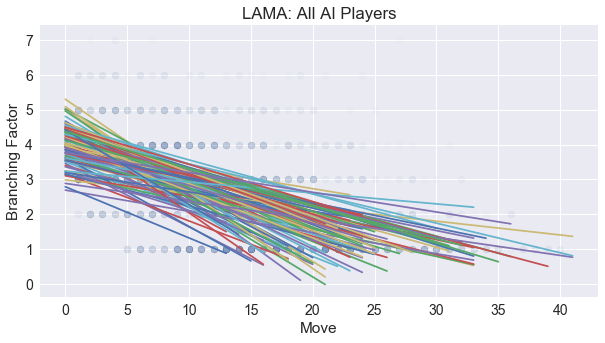
Convergence = 0.58
LAMA has the highest convergence value yet! Here we can see the regression lines for each game plotted on top of a scatter plot of the branching factors versus the move in the game. We see a definite slope downward as the game progresses, as many players who dropped out of the game are only given the one choice to pass.
As with some other games, the length of a LAMA round is determined by its players. When we crunch the statistics from our simulations to generate the following graph comparing game length and number of players, we can make two conclusions.
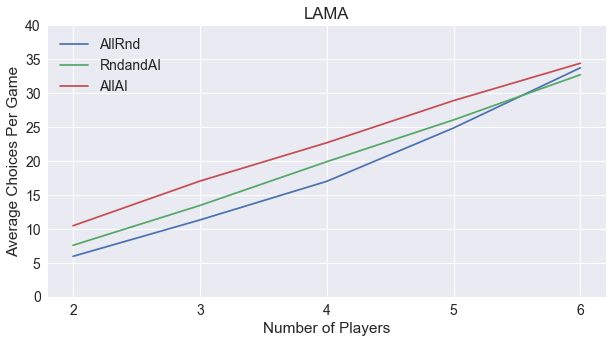
First, the length of a round of LAMA grows linearly with the number of players, unlike Pairs and Ninety-Eight, where the game length was independent. For each player added, it appears there will be 7 more choices made.
Second, the AI players add a little bit of length to the game! With one AI player, there are about 2 more choices than the all random simulations, and with all AI players, there are about 5 more choices. With 6 players, these trends break down, but I’m going to attribute that to statistical fluctuations and not a true trend.
Spread = 0.17
Now to examine the lead histories, a record of the rank estimates that each AI player makes as they choose their moves throughout the round. Here we see a long four-player round.
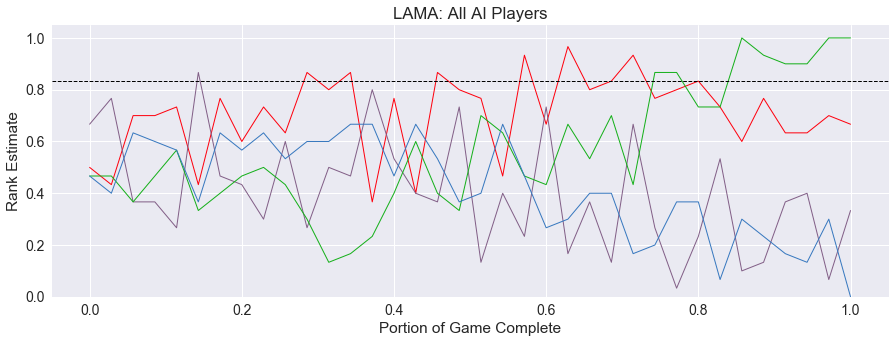
The players estimate their chances of winning evenly for much of the round, only settling their ranks in the last quarter of play.
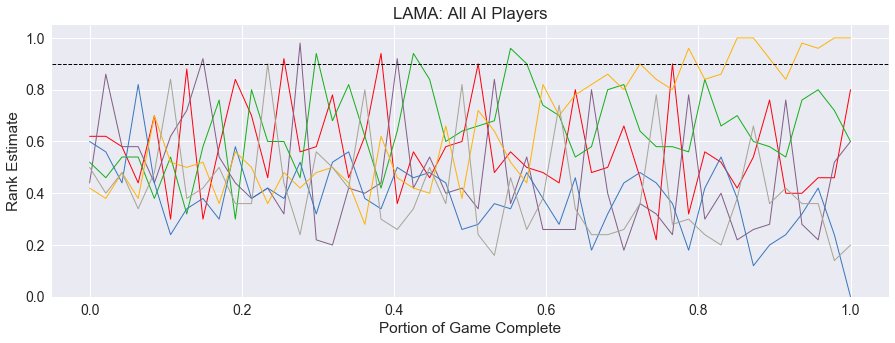
This unsettled feeling is present no matter the number of players. Below is a sample round with 6 players with the same variability in rank estimates.
Similarly, we can see a two-player round with a rocky midgame.
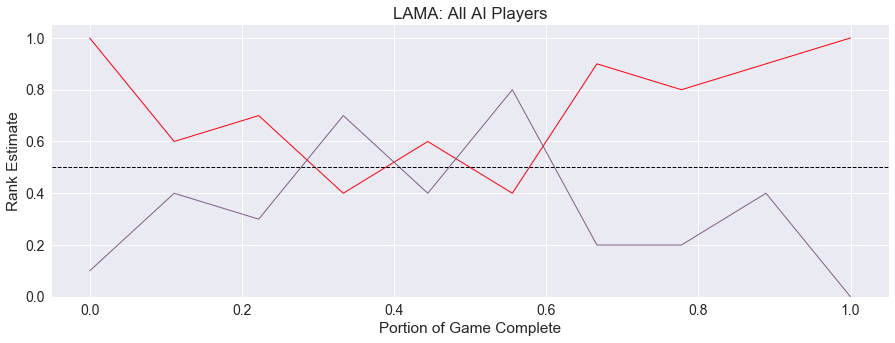
The spread of choices is in line with the previous games of Pairs, Hearts, and Stealing Bundles. Players can usually find an interesting move to make among their choices, but there is not enormous variety.
Drama = 0.49
Let’s look at the full lead history graph for all 100 simulations. The following graph is for a four-player round, colored so the first player is red, the second is purple, third is green, and fourth is blue.
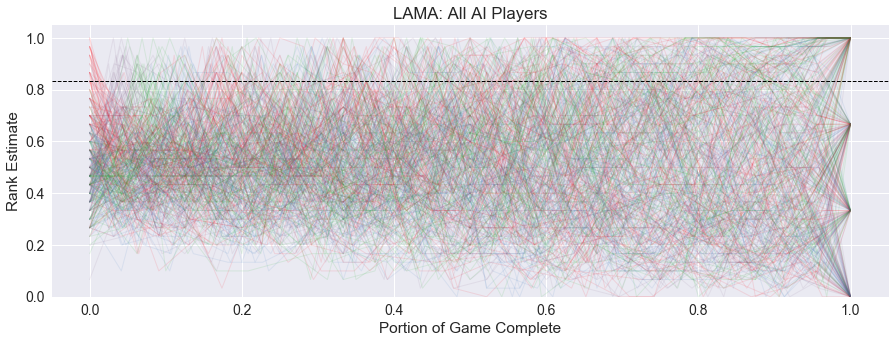
It is harder to see because of the variable round length, but there is definitely a regular pattern of overestimation happening in the beginning of each round. The peaks in the graph cycle at least one round of red, purple, green, and blue, before the pattern is lost to the details of each round.
But other than the initial cycle, it is hard to see if there is anything else interesting happening. Frankly, it looks like a terrible mess of a graph!
With the increased variability we see in the lead history, we would expect these rounds of LAMA to be somewhat dramatic, measuring the magnitude of how low the eventual winner was in this graph. The next graph shows the winner in red, and all other players in black.
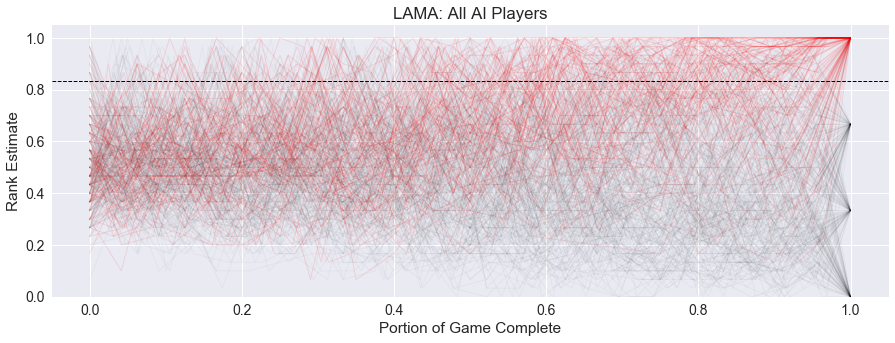
LAMA does score well on drama at 0.49. In the second half of the round, we can see a general rise to the winner’s estimates. But these do not consistently stay high, thus the drama.
Security = 0.26
Our last heuristic is Security, measuring how often the winning player believes they are in the lead for the round. To better visualize the security heuristic, I’m going to use the average trend graphs I last used to compare Hearts variants. Here is the four-player graph we discussed above, with the average trend for each rank plotted on top.
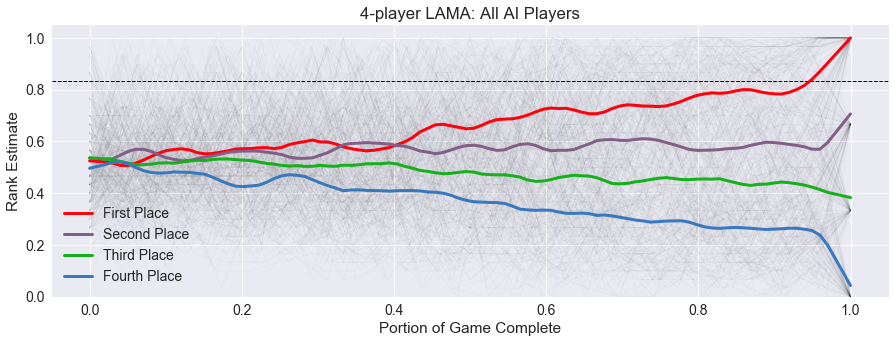
While the above graph looked like a mess, this gives us a clearer picture of what is happening in the round. There is a divergence around half-way through the game into separate ranks, however, there is still opportunity for movement between the ranks.
Also, we see a sharp resolution into fixed ranks at the end of the round. This means that in many rounds, it is not until the last turn that the ranks are completely determined. This is because much of the information needed to make a good estimate is hidden in the face-down or held cards of other players. Our AI players are excellent card counters, but do not make any inferences about what might be in another player’s hand based on their behavior.
Is this trend the same across all player counts? Shown below are the average trend graphs for the two-player games and three-player games.
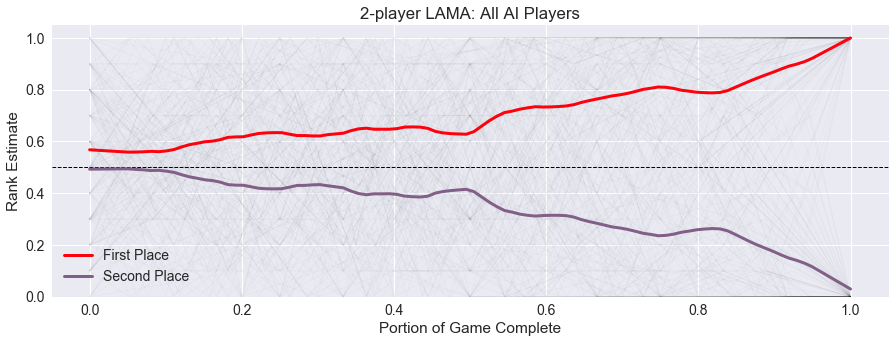
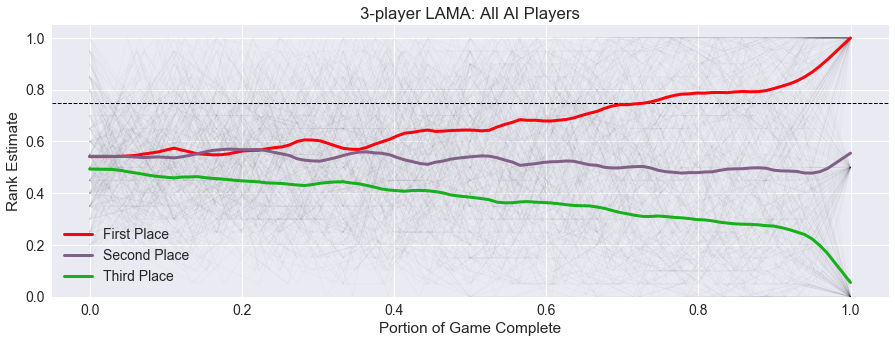
While there is still some element of surprise and drama at the end of these rounds, the players separate into ranks earlier and have much higher levels of security.
For the five and six-player games, shown below, the scores are much tighter throughout, with little if any security for the winning player.
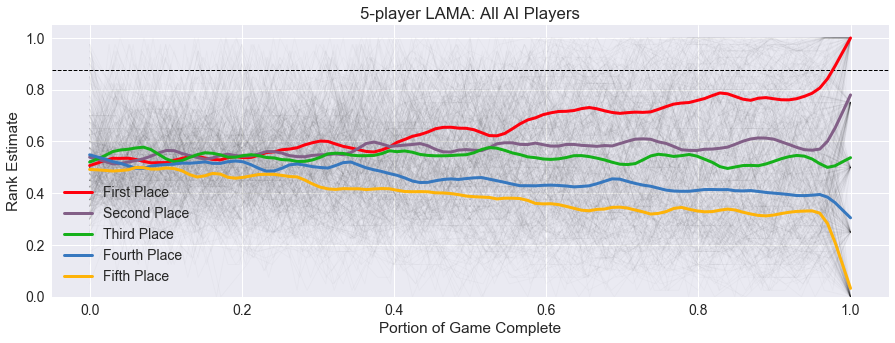
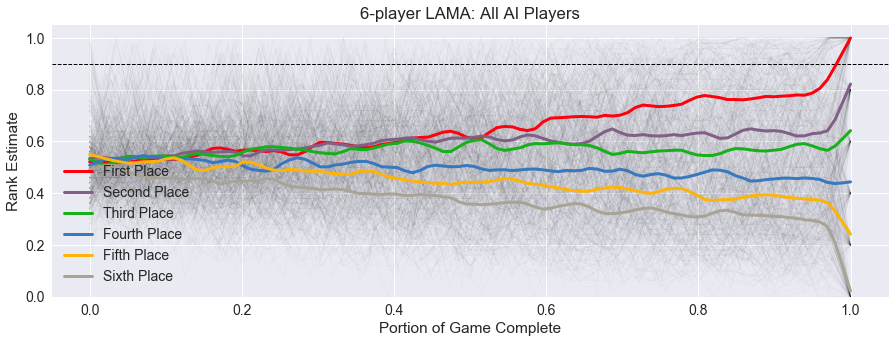
With more players in the round, the contents of other player’s hands are even more shrouded in mystery. Although in each round, there is a wider separation between the first and second-place players than between the subsequent rankings, showing that the winner is able to pick up on their success to some degree.
Summary
Here is our summary graph of all the heuristics for one round of LAMA in the four-player simulations, showing visually the low spread, high fairness, and mild security we found above.
Up Next - Full Game
With a handle on some of the basics of how LAMA rounds work, our next post will explore full games of LAMA up to the intended 40 points. How will this change the game play experience we are seeing in this post? Is the incentive to deduct points when finishing a round without cards enough to push players to be risky and draw more cards?
These full simulations will take a while to run and crunch the data, so hopefully I will have the next post up in a week or two. Thanks for reading!
comments powered by Disqus

