
Stealing Bundles mixed up a repeated deal and matching mechanics, with some timing and competition for the other player’s points. Given our statistical analysis, let’s see how it scores on our heuristics of Fairness, Convergence, Spread, Drama, and Security.
(See this previous post for a review of the heuristics I’ll be discussing.)
Fairness = 0.88
With games using just random players, we can determine if Stealing Bundles exhibits some bias toward the first player, either favorably or unfavorably. And as we have found for other games, this game is mostly fair. The image below shows that random players behave as expected.
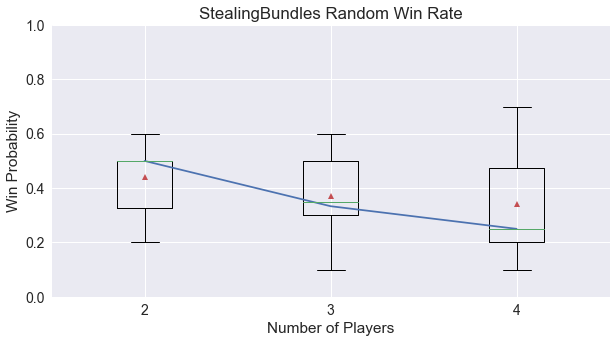
However in the four-player game, there is an indication that the first player will win more often than average. More simulations could help determine if this is random fluctuations or a true bias.
Convergence = 0.51
Since the number of playable cards decreases each round by one, we expect Stealing Bundles to display some convergence, however, this is tempered by the repeated dealing in the middle of the game. Here I’ve added in the regression line for Stealing Bundles to our graph of player choices, and it reflects this slight downward compression toward the end of the game.
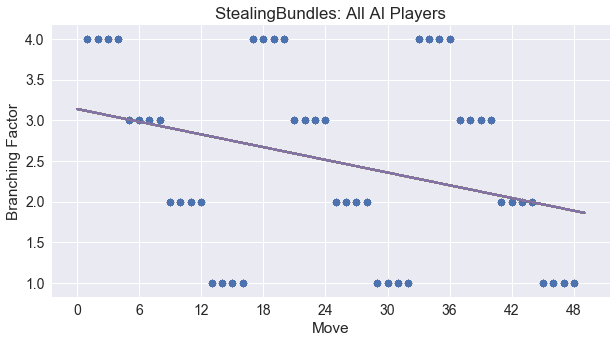
Spread = 0.14
Do players have interesting choices in Stealing Bundles? The spread for this game is fairly low, meaning that many of the choices in the game look similar to the player. Below we show a sample lead history graph for Stealing Bundles from a four-player game with all AI players. In this game, all players think they are doing reasonably well for most of the game, and estimate that other players are also doing well, as we can see from the tight band of ranks between 0.4 and 0.7. There is little to distinguish the players until the last fifth of the game when the ranks are finally settled.
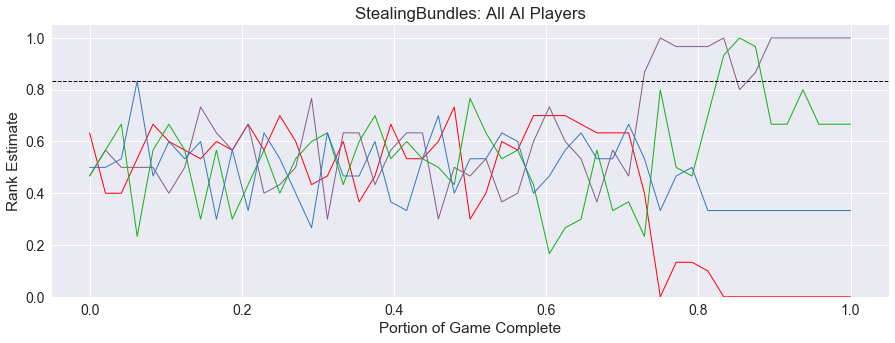
Drama = 0.51
We can start to see some trends for the Stealing Bundles when looking at the aggregate lead histories. First, we see below the lead histories for the four-player games where only one player was an AI, and the rest were making random decisions.
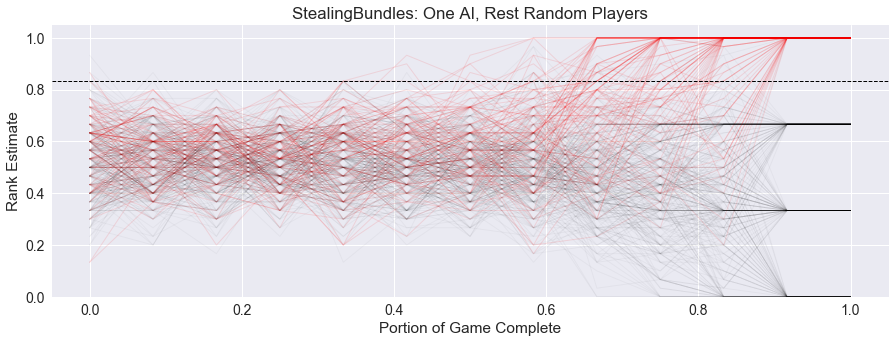
There is a clear difference between the first third, second third, and final third of the game, which lines up with when new cards are dealt to the players. In the second third, we see the emergence of players believing they can win the game, moving their estimates up to near the top, and this is solidified in the final third of the game, when all cards have been dealt.
The drama for Stealing Bundles is higher than the other games we have investigated, mostly due to the uncertainty in the first two-thirds of the game. This trend is born out in the games where all players are AI, as shown below. Each player in the game is denoted with a different color based on their turn order, red for 1st, green for 2nd, cyan for 3rd, and magenta for 4th.
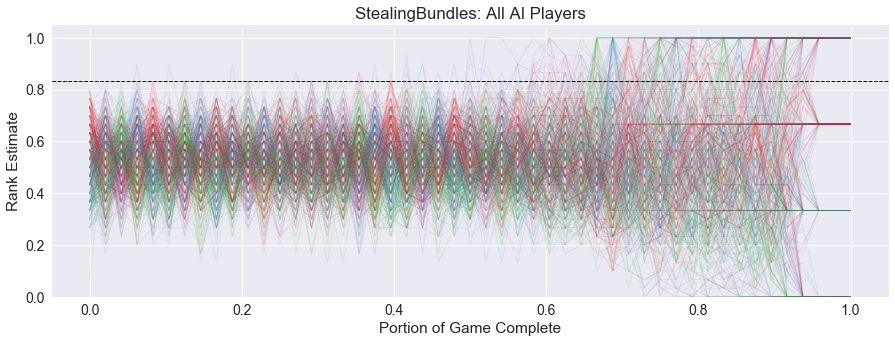
There is a repeating pattern where the players to over-estimate their own success on their turn and underestimate everyone else. The peaks in this graph repeat in player order: red, green, cyan, magenta, red, green, etc… This could be due to the true distribution of scores being much tighter, around 0.75 for each player, in the early part of the game, but the AI players are picking a statistical outlier where they look good in comparison to the others. The pattern fades but then picks up again when players are dealt more cards at the one-third mark. We do not see the pattern reemerge at the two-third mark though, because by then players are starting to get a better estimate of their chances of winning. This pattern also increases the drama of the game, since other players are consistently underestimating the winner for the first portion of the game.
Security = 0.19
With the relative uncertainty for two-thirds of the game, Stealing Bundles has the lowest value for Security yet. In the four-player games show below, we can see the winner becoming clear after the last round of cards are dealt to the players, but even then, there remains some movement in the ranks for some games. In other runs, the ranks are completely determined by this final card deal, establishing the solid bands of rank for first, second, third, and fourth player.
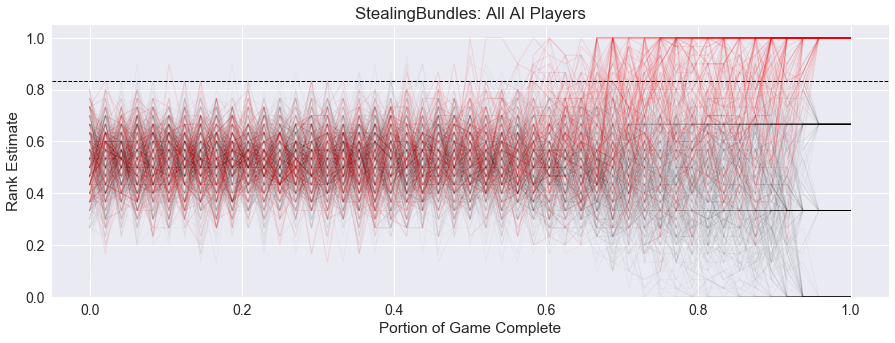
For completeness, here is the three player graph:
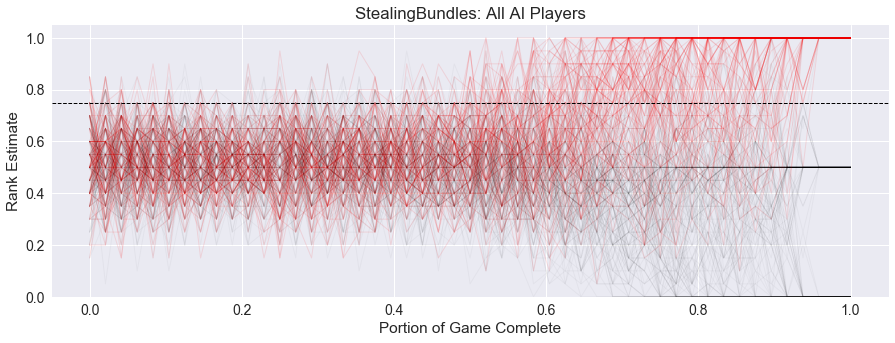
and the two-player graph:
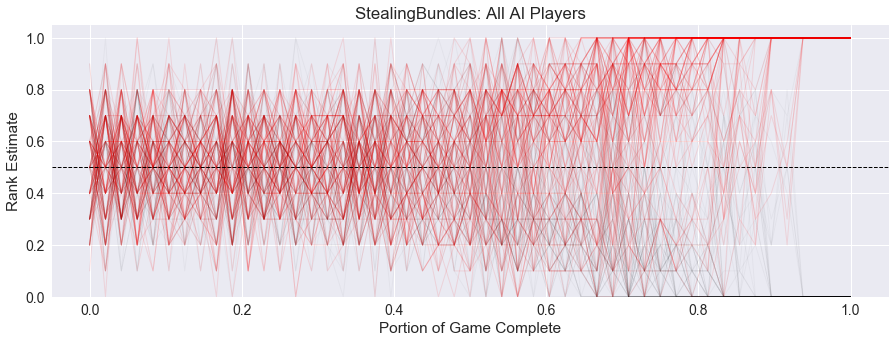
There appears to be a little more control in the game with less players, as the winner trends upward and starts to diverge from the other players starting around 50% of the game for two and three players, but is delayed until 60% of the game for four players.
Summary
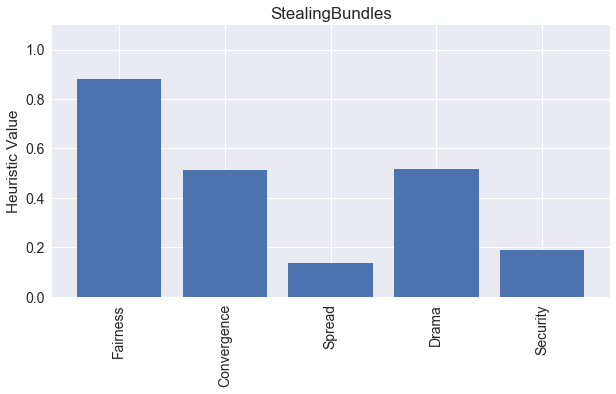
Here is our summary graph of all the heuristics for Stealing Bundles. Fairness remains high, with a slight convergence. (Convergence might need to be recalibrated, as even games with a strong slope appear to be close to 0.5 when scored.) There is a tight Spread of scores for the AI players, which is related to an increase in Drama, and a decrease in Security.
Up Next - Hearts
Four games in four different genres so far! Our next game will be a return to trick-taking games with the classic Hearts. With such a familiar game, I’m hoping to hear from you about your questions and hypotheses to explore. There are a large number of variants that we can simulate, and hopefully we will see some empirical evidence of their relative success or failure to add interest to the game play. Please add in what you would like to see me cover as we survey Hearts in future posts and I’ll try to run simulations to answer them. Thanks for reading!
comments powered by Disqus

