
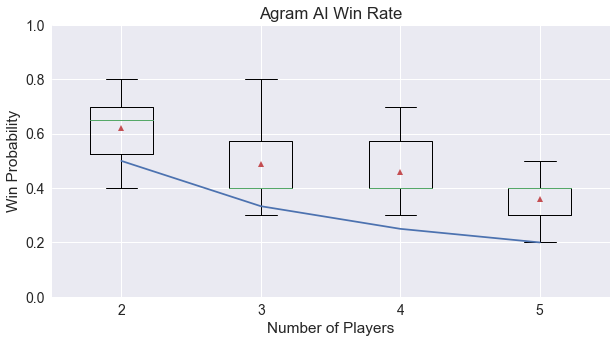
Time for a new heuristic! For each game analyzed so far, I’ve been able to say that AI players can win against random players, demonstrating there is some strategy in the game. But can we start to place a metric on how successful the AI players are? In a game like Agram, the AI was successful, but barely as seen here:
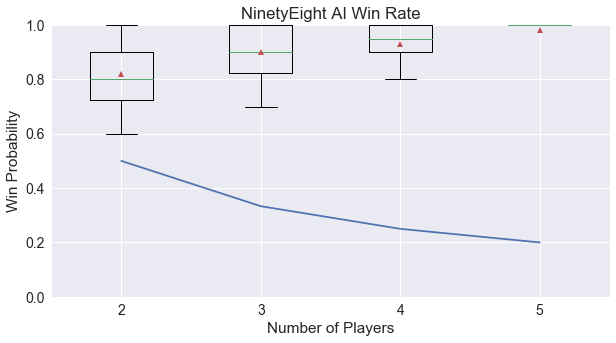
But in Ninety-Eight, the AI could win against random players in most simulations:
Essentially, we want to see how much control a player has over their own fate, or if they are at the whims of random events. This needs to be more than just the AI win percentage, and should take into account the expected performance of the random player as a baseline. We will call this new heuristic Order, a positive spin on the chaos found in many card games.
Order
First, we record the win percentage (aiwp) of the AI player in games with one AI player and the rest Random players.
Next, we need to find the expected win percentage (ewp) for the number of players in the game, assuming that the game is fair. For example, with 4 players, a fair game would have the first player win 25% of the time.
A perfect AI in a perfect information world should be able to win 100% of the games. This is reduced as chaos is introduced that the AI cannot account for. Therefore, we can calculate the Order of the game by finding the ratio of the aiwp gain over the perfect ordered AI gain as follows:
\[Order = \frac{aiwp - ewp}{1 - ewp}\]Order will be a value between 0 and 1. When this number is low, then the AI player has a hard time winning against a random chaotic player, but when it is high, the AI player is very successful in determining their success in the game.
For the above games when played with four players, Agram scores a 0.19, while Ninety-Eight scores 0.88. I’ve added in this heuristic to the summary page for each game discussed so far.
Up Next
Back to discussing Hearts! It is heuristic time and lead history graph, and look out for some unexpected findings related to “Shooting the Moon!”
comments powered by Disqus

