For our next analytical approach to The Wheel of Time series, following word clouds and character rankings, we will look at how to cluster the novels. This will involve a few steps:

• Converting the novels into vectors
• Finding similarity between these vectors
• Clustering books based on similarity

As before I’ve linked to another Jupyter Notebook, although the details are missing from this one because I used it as a lab assignment in the course. Some of what I implement is loosely based on another tutorial about document clustering.

Conversion to Vectors

When we usually think of finding how related items are, we look at them across a number of dimensions and calculate their distance. For two points on a map, we might find their latitude and longitude as their dimensions, and the calculate the great-circle distance. How do we do this with our novels?

First, we need to break the text down into words, and again calculate the term frequency. Each word can be though of as a dimension, and the frequency is the data for that dimension. If one novel does not have some words that appear in other novels, then we give those dimensions a word count of 0. We’ll call these term-frequency vectors.

But this has a few issues. First, most of the novels will look very similar, because they are all using English, and as we saw earlier, they tend to follow Zipf’s Law. This is OK if we are interested in the subtle differences in word choice across the novels, but if we are looking for content, we need to refine our vectors. We could again remove the stop words, but it turns out there is a more relaxed and localized way to approach this problem, called tf-idf.

In addition to the Term Frequency (tf) for each word, we can calculate the Inverse Document Frequency (idf) (thus the name tf-idf vectors). The big picture is that count for each word is reduced as the word is found to be common across the corpus, in our case, the whole Wheel of Time series. This will heavily discount the common English words, but also eliminate common words relative to our series, such as Rand, Aes Sedai, etc, whereas words that only appear in a few of the books will retain their high frequency counts. Each book then is represented by what makes it unique in the series.

Similarity Metric

The second issue is that our novels are different lengths. If we compare these vectors with distance metrics such as the Euclidean distance from algebra, we might find that two books which use the same words with the same frequency are very far apart, because one book is much longer than the other. More often in NLP, we see the Cosine similarity metric. Instead of calculating the distance between two points, we are calculating the size of the angles between two vectors, making the magnitude of the vectors irrelevant. Here’s a great tutorialon when to use Cosine similarity.

Clustering Algorithm

Finally, with the novels all encoded as vectors, and our similarity metric decided, we can start to cluster the novels. For this work, I used UPGMA Clustering, a bottom-up hierarchical method.

• Every book starts in its own cluster
• While we still have multiple clusters
  • Find the nearest two clusters according to Cosine similarity
  • Join these two clusters to make a new cluster
  • Recalculate the distances for the remaining clusters.

You can implement this yourself, like we did in class, or use the scipy clustering library. This library also includes functionality to draw a dendrogram based on the UPGMA algorithm.

So, did we find any interesting patterns?

Spoiler Alert!

Discussions of plot points and threads across the whole series follow. Please take appropriate cautions if this is important to you.

Content Clustering

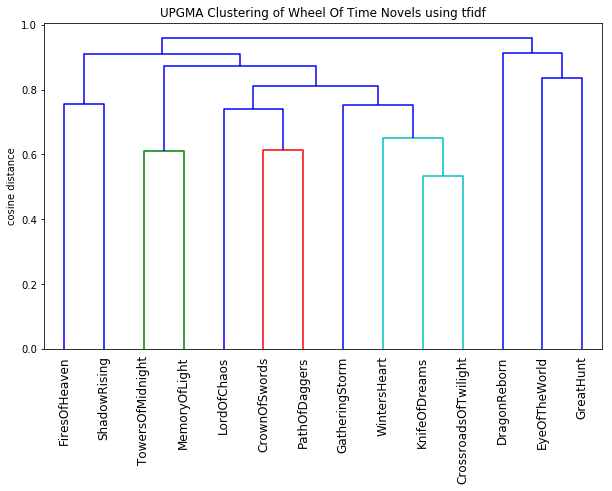
First, let’s look at clustering based on the tf-idf vectors, where books are represented by words that appear less frequently across the whole series. We can see that there appear to be five main clusters in the series, and this clustering matches the content, and the narrative progression, of the series. A few things stand out to me. On the right are the first three novels in the series, covering the initial Emond’s field crew working their way out into the world with a relatively stable cast of characters. The closest two novels are Crossroads of Twilight (the novel where nothing happens) and Knife of Dreams, which wraps up many of these lingering plot lines. These two books are in a cluster with Winter’s Heart, the which serves as a lead in for the focus on the Mat, Perrin, Egwene, and Elayne plotlines, and The Gathering Storm, which bridges their resolution with the concluding two novels, Towers of Midnight and A Memory of Light. The Shadow Rising and the Fires of Heaven are the most distant after the first three novels, perhaps because of their unique settings of the Aiel waste and other locations?

Word Choice Clustering

If we use the initial term frequency vectors without discounting common words, we see a very different story emerge. Remember, these vectors help us see similarities and differences in word choice and writing style, what I call the “glue” words of our language.

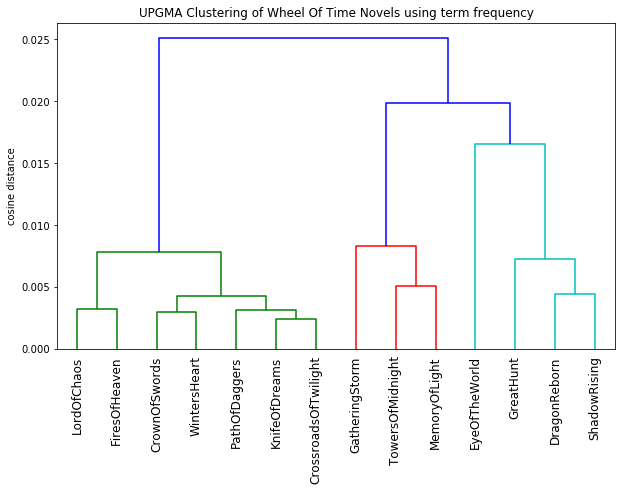
The most unique book in the series is The Eye of the World. And it appears as the series progresses, the language becomes more and more homogeneous, with the later novels forming very tight clusters. But here is where things get very interesting for me. Robert Jordan passed away before completing the series, and Brandon Sanderson was brought in to finish the last three books. We can see evidence of this in the dendrogram, where The Gathering Storm, Towers of Midnight, and A Memory of Light are tightly connected and colored in red. And rather than try to match the style of writing Jordan had settled on in his later books, his style has echoes of the earlier novels. Could this be a contributing factor to the warmer reception these last three novels received?

Conclusion

With just a bit of math and some algorithms, we were able to confirm the large epic plot points of the series and uncover some hidden relationships of writing style and authorship. Are there other long series that might have the same structure? If you’re a fan of the Wheel of Time series, what other insights can you see from these graphs?