With Agram coded in RECYCLE, we can run many simulations in CardStock with both random and AI players to try and understand how the game works. Random players make a choice in the game using a uniform distribution across each choice, while the AI players use statistics of random simulations for each choice to determine their best chance of winning. The AI strategy we use most often is called a Perfect Information Pure Monte Carlo Player (PIPMC).
Our AI player will estimate the best move in a very simple manner. It will try out each move, followed by running a bunch of random simulations to the end of the game and see if it wins. It average these results for each move, and will pick the move that looks to have the best chance of winning with these estimates.
To gather statistics on the game, we ran 100 games with all random players, 100 games with one AI and the rest random players, and 100 games with all AI players. Let’s see if we can answer some basic questions about the game.
Are there sufficient choices for players?
The below image shows the average number of moves a player has on each turn, called the branching factor, in a four-player game using random players.
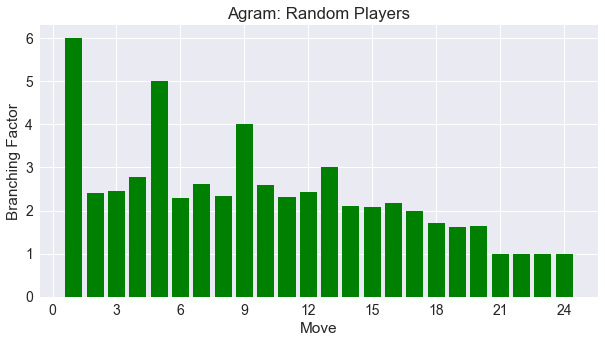
There’s a repeated peaking pattern, every four moves, which lines up with the lead player of the trick. The lead player can always play whatever card they desire, but subsequent players must follow suit or discard. It is easier to understand a summary graph, aggregated depending on the player’s turn order in relation to the lead player for each trick.
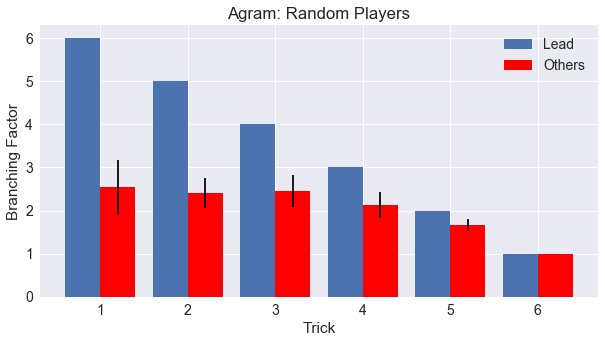
We can see the effect of being forced to follow suit when possible. Following players are limited to approximately 2.5 card choices on average for the first three tricks and tapering off thereafter. I’ve added in error bars to help see the spread of data, calculated by dividing the 100 simulations into 10 groups, averaging each result, then calculating the standard deviation of these averages. So, according to this data, there is a definite advantage to being in the lead player in terms of player choice.
Can players be strategic in Agram?
To investigate the potential for strategy in Agram, we ran 100 simulations for each of 2 through 5 players, using one AI player with the remaining players random. Hopefully, we can see that an AI player is able to beat random players.
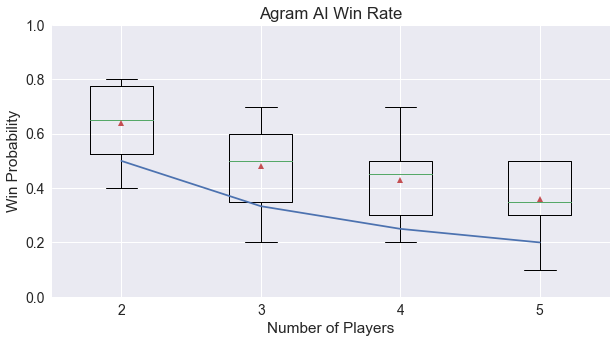
We can see above the win percentage for the AI player in comparison to the expected probability of winning for a random player, given the assumption that the game is balanced. AI players are able to control their fate, outperforming the expected value by approximately 20 percentage points across all player sizes. However, there is still enough randomness in the game to confound their ability to win.
Up Next
We’ve seen some aggregate information about the game so far, but what does it look like to actually play the game? Can a player tell when they are winning in Agram? Is Agram a fair game for all players? We’ll need to explore some advanced heuristics next and dive in to details on how the AI behaves when it plays. Stay tuned!
comments powered by Disqus

