Binary Search Tree Traversal Algorithm
Goals
Students will understand elements of the traversal algorithm for binary search trees.
Video
Materials
One deck of Acorn cards.

Setup
Shuffle the deck and deal each student 9 cards.
Each student will shuffle their 9 cards, and then create a binary tree as demonstrated on the insertion algorithm page.
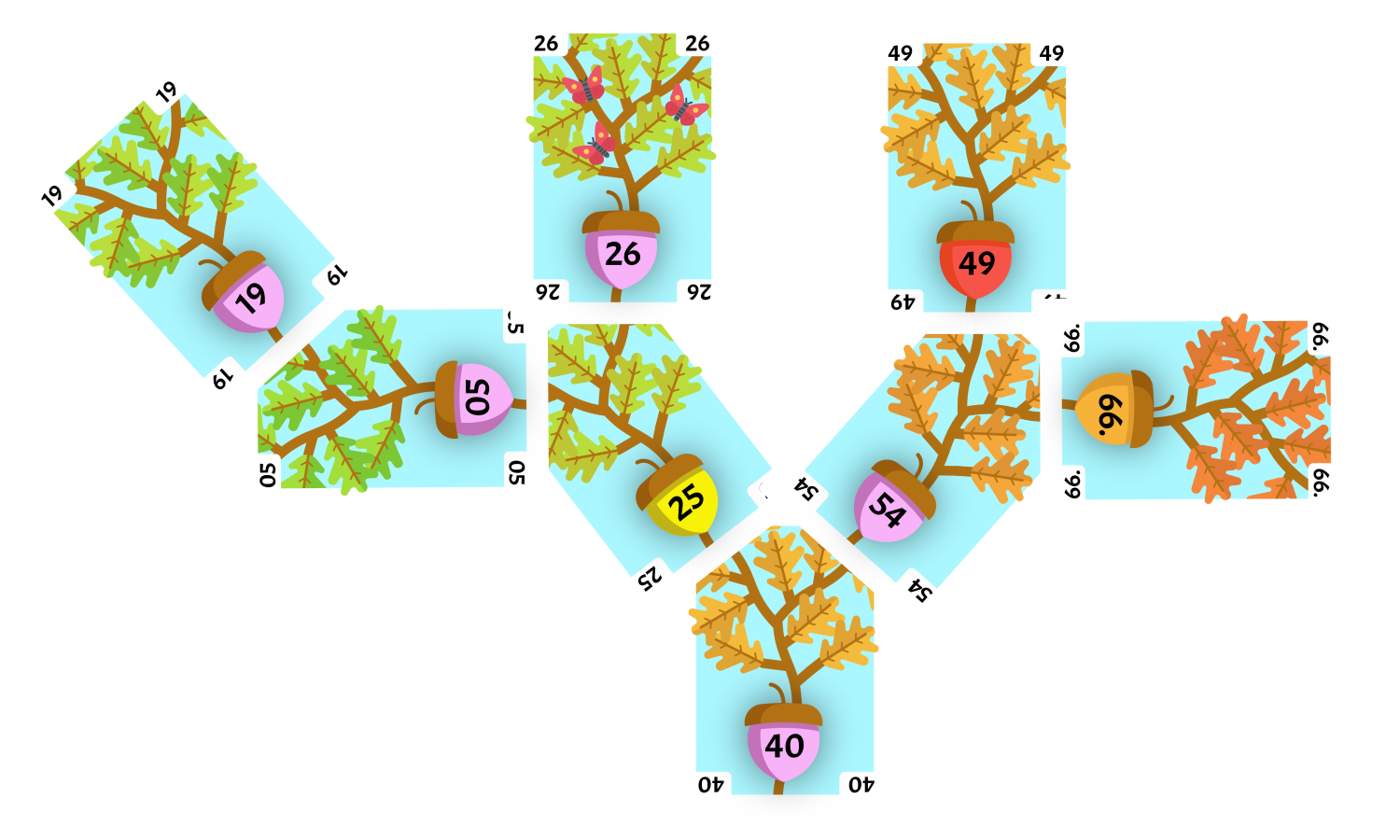
Algorithm
There are three possible Algorithms for traversing a tree: preorder, postorder, and inorder. For all Algorithms we will start at the root of the tree as our current node, and keep a record of values for the nodes we visit.
Preorder
-
Record the value of the current node.
-
If the left child of the current node is the root of a subtree, the left child will now be our new current node and return to step 1. Otherwise, record the value of the left child.
-
If the right child of the current node is the root of a subtree, the right child will now be our new current node and return to step 1. Otherwise, record the value of the right child.
-
If the current node has a parent, the parent will now be our new current node. If the current node is the root of the tree and both of its children have been recorded, we are finished. Otherwise, return to step 3.
Postorder
-
If the left child of the current node is the root of a subtree, the left child will now be our new current node and repeat step 1. Otherwise, record the value of the left child.
-
If the right child has already been recorded, go to step 3. If the right child of the current node is the root of a subtree, the right child will now be our new current node and return to step 1. Otherwise, record the value of the right child.
-
Record the value of the current node. If the current node has a parent, the parent will be our new current node and return to step 2. Otherwise, we are finished.
Inorder
-
If the left child of the current node is the root of a subtree, the left child will now be our new current node and repeat step 1. Otherwise, record the value of the left child.
-
If the value of the current node has not been recorded yet, record the value of the current node. Otherwise, we are finished.
-
If the right child of the current node is the root of a subtree, the right child will now be our new current node and return to step 1. Otherwise, record the value of the right child.
-
If the current node has a parent, the parent will be our new current node and return to step 2.
Example
Preorder

We will start at the root of our tree 40 as our current node. Our list of values is currently [].
Step 1. We will record the value of the current node. Our list of values is now [40].
Step 2. The left child of our current node, 25, is a root of a subtree, so 25 will be our new current node and we will return to Step 1.
Step 1. We will record the value of the current node. Our list of values is now [40, 25].
Step 2. The left child of our current node, 05, is a root of a subtree, so 05 will be our new current node and we will return to Step 1.
Step 1. We will record the value of the current node. Our list of values is now [40, 25, 05].
Step 2. There is no left child of our current node, so it can not be a root of a subtree and there is no value to record.
Step 3. The right child of our current node, 19, is not a root of a subtree, so we will record the value of the right child. Our list of values is now [40, 25, 05, 19].
Step 4. The current node has a parent, 25, so 25 will be our new current node and we will return to Step 3.
Step 3. The right child of our current node, 26, is not a root of a subtree, so we will record the value of the right child. Our list of values is now [40, 25, 05, 19, 26].
Step 4. The current node has a parent, 40, so 40 will be our new current node. 40 is the root of the tree, but we have not recorded the right child of 40 so we will return to Step 3.
Step 3. The right child of our current node, 54, is a root of a subtree, so 54 will be our new current node and we will return to Step 1.
Step 1. We will record the value of the current node. Our list of values is now [40, 25, 05, 19, 26, 54].
Step 2. The left child of our current node, 49, is not a root of a subtree, so we will record the value of the left child. Our list of values is now [40, 25, 05, 19, 26, 54, 49].
Step 3. The right child of our current node, 66, is not a root of a subtree, so we will record the value of the right child. Our list of values is now [40, 25, 05, 19, 26, 54, 49, 66].
Step 4. The current node has a parent, 40, so 40 will be our new current node. 40 is the root of the tree and we have recorded both children of 40, so we are finished.
Our final list of values after the Preorder Algorithm is [40, 25, 05, 19, 26, 54, 49, 66].
Postorder

We will start at the root of our tree 40 as our current node. Our list of values is currently [].
Step 1. The left child of our current node, 25, is a root of a subtree, so 25 will be our new current node and we will repeat Step 1.
Step 1. The left child of our current node, 05, is a root of a subtree, so 05 will be our new current node and we will repeat Step 1.
Step 1. There is no left child of our current node, so it can not be a root of a subtree and there is no value to record.
Step 2. The right child of our current node, 19, has not been recorded, and is not a root of a subtree, so we will record the value of the right child. Our list of values is now [19].
Step 3. We will record the value of the current node. The current node has a parent, 25, so 25 will be our new current node and we will return to Step 2. Our list of values is now [19, 05].
Step 2. The right child of our current node, 19, has not been recorded, and is not a root of a subtree, so we will record the value of the right child. Our list of values is now [19, 05, 26].
Step 3. We will record the value of the current node. The current node has a parent, 40, so 40 will be our new current node and we will return to Step 2. Our list of values is now [19, 05, 26, 25].
Step 2. The right child of our current node, 54, has not been recorded, and is a root of a subtree, so 54 will be our new current node and we will return to Step 1.
Step 1. The left child of our current node, 49, is not a root of a subtree, so we will record the value of the left child. Our list of values is now [19, 05, 26, 25, 49].
Step 2. The right child of our current node, 66, has not been recorded, and is not a root of a subtree, so we will record the value of the right child. Our list of values is now [19, 05, 26, 25, 49, 66].
Step 3. We will record the value of the current node. The current node has a parent, 40, so 40 will be our new current node and we will return to Step 2. Our list of values is now [19, 05, 26, 25, 49, 66, 54].
Step 2. The right child of our current node, 66, has been recorded, so we will go to Step 3.
Step 3. We will record the value of the current node. The current node does not have a parent, so we are finished. Our list of values is now [19, 05, 26, 25, 49, 66, 54, 40].
Our final list of values after the Postorder Algorithm is [40, 25, 05, 19, 26, 54, 49, 66].
Inorder

We will start at the root of our tree 40 as our current node. Our list of values is currently [].
Step 1. The left child of our current node, 25, is a root of a subtree, so 25 will be our new current node and we will repeat Step 1.
Step 1. The left child of our current node, 05, is a root of a subtree, so 05 will be our new current node and we will repeat Step 1.
Step 1. There is no left child of our current node, so it can not be a root of a subtree and there is no value to record.
Step 2. The value of our current node has not been recorded, so we will record the value of the current node. Our list of values is now [05].
Step 3. The right child of our current node, 19, is not a root of a subtree, so we will record the value of the right child. Our list of values is now [05, 19].
Step 4. The current node has a parent, 25, so 25 will be our new current node and we will return to Step 2.
Step 2. The value of our current node has not been recorded, so we will record the value of the current node. Our list of values is now [05, 19, 25].
Step 3. The right child of our current node, 26, is not a root of a subtree, so we will record the value of the right child. Our list of values is now [05, 19, 25, 26].
Step 4. The current node has a parent, 40, so 40 will be our new current node and we will return to Step 2.
Step 2. The value of our current node has not been recorded, so we will record the value of the current node. Our list of values is now [05, 19, 25, 26, 40].
Step 3. The right child of our current node, 54, is a root of a subtree, so 54 will be our new current node and we will return to Step 1.
Step 1. The left child of our current node, 49, is not a root of a subtree, so we will record the value of the left child. Our list of values is now [05, 19, 25, 26, 40, 49].
Step 2. The value of our current node has not been recorded, so we will record the value of the current node. Our list of values is now [05, 19, 25, 26, 40, 49, 54].
Step 3. The right child of our current node, 66, is not a root of a subtree, so we will record the value of the right child. Our list of values is now [05, 19, 25, 26, 40, 49, 54, 66].
Step 4. The current node has a parent, 40, so 40 will be our new current node and we will return to Step 2.
Step 2. The value of our current node has been recorded, so we are finished.
Our final list of values after the Inorder Algorithm is [05, 19, 25, 26, 40, 49, 54, 66].