Splay Tree Algorithm
Goals
Students will understand elements of the insertion algorithm for splay trees.
Video
Materials
One deck of Acorn cards.

Setup
Shuffle the deck and deal each student 6 cards.
Each student will shuffle their 6 cards, and place them in a face-down pile to their left.
Algorithm
Flip the top card face-up, and place this card directly in front of you. This card will be known as the root card.
For the remaining cards, flip each one face-up in turn, calling it the flipped card. You will now insert this card into your tree.
Start each card insertion by labeling the root card as the current card.
Where To Look
-
If the flipped card is less than the current card, look at the upper-left corner of the current card.
-
Otherwise the flipped card must be greater than the current card, so look at the upper-right corner of the current card.
Can I Place
-
If a card is found where you are looking, repeat the Where To Look step again with the found card becoming the current
-
Otherwise, if there is no card where you are looking, place the flipped card on this corner, tilted roughly 45 degrees from the current card. Go to the Splay portion.
Splay
-
If the flipped card is a child of the root card, go to the Zig portion.
-
If the flipped card and the parent of the flipped card are both right children or both left children, go to the Zig-Zig portion.
-
If the flipped card and the parent of the flipped card are opposite children (i.e one is a left child, one is a right child), go to the Zig-Zag portion.
Zig
-
If the flipped card is a left child, go to the rotate portion and perform a right rotation with the flipped card as the current card.
-
If the flipped card is a right child, go to the rotate portion and perform a left rotation with the flipped card as the current card.
Zig-Zig
-
If the flipped card and the parent card of the flipped card are both left children, go the rotate portion and perform a right rotation with the parent card as the current card, then perform a right rotation with the flipped card as the current card.
-
If the flipped card and the parent card of the flipped card are both right children, go the rotate portion and perform a left rotation with the parent card as the current card, then perform a left rotation with the flipped card as the current card.
Zig-Zag
-
If the flipped card is a left child, go the rotate portion and perform a right rotation with the flipped card as the current card, then perform a left rotation with the flipped card as the current card.
-
If the flipped card is a right child, go the rotate portion and perform a left rotation with the flipped card as the current card, then perform a right rotation with the flipped card as the current card.
Rotate
The parent of the current card is the rotate card.
-
Replace the side of rotation child of the current card with the rotate card. Keep all of the rotate card children on the side of rotation intact. Set aside the side of rotation child and keep all of the children intact. If the rotation was done on a subtree, place the current card where the rotate card used to be. Keep all of the current card children intact.
-
Place the side of rotation child of the current card that was replaced in step 1 as the opposite side of rotation child of the rotate card.
If a Zig, Zig-Zig, or Zig-Zag step finishes and the flipped card is not the root of the tree, return to the Splay portion.
Example
Add 26
The first card flipped up is 26. Place this in front of you be the root card.

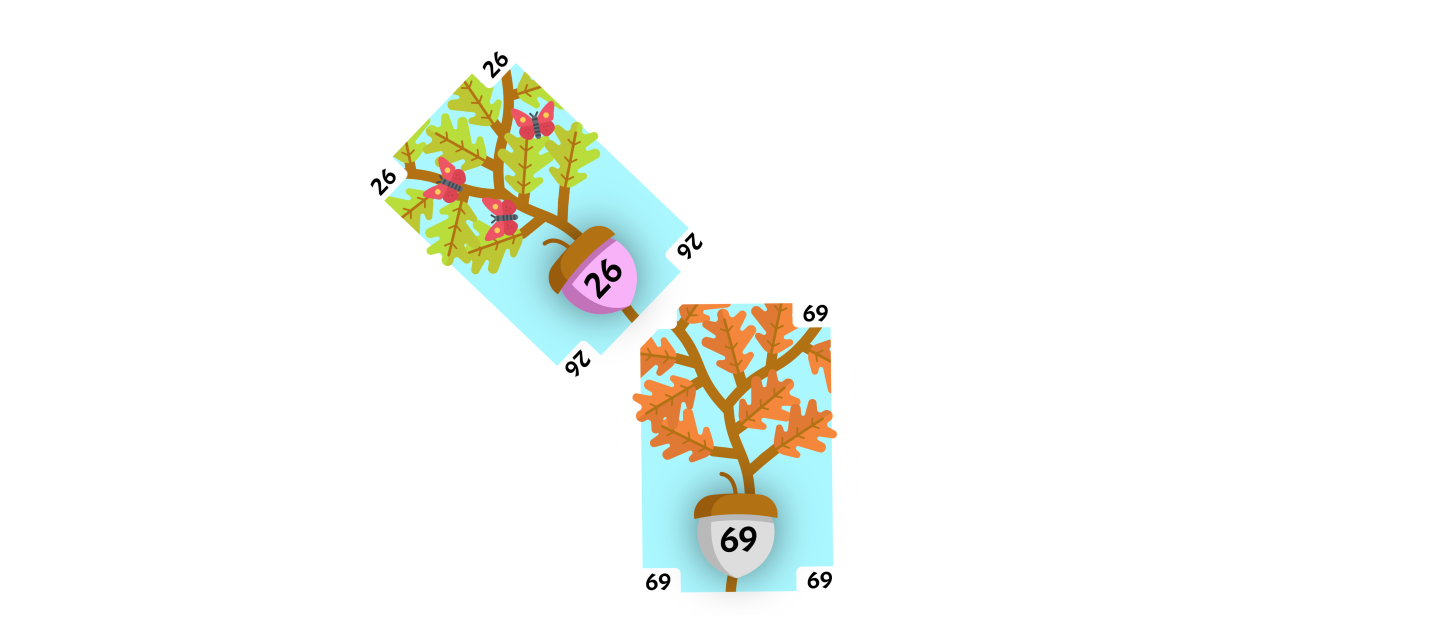
Add 69
The next card flipped up is the 69. We compare it to the root and determine that it is less than the root, so we look at the upper-left corner.
There is no card in this corner, so we can place the card on this corner.

Since the flipped card 69 is a child of the root card we will perform a Zig operation. Since the flipped card is the right child of the root card, we will perform a left rotation with the flipped card as our current card. The parent of our current card 26 will be our rotate card.
The rotate card will replace the left child of the current card. The current card had no child so the rotation is finished. The flipped card 69 is now the root of the tree and we do not need to Splay again.
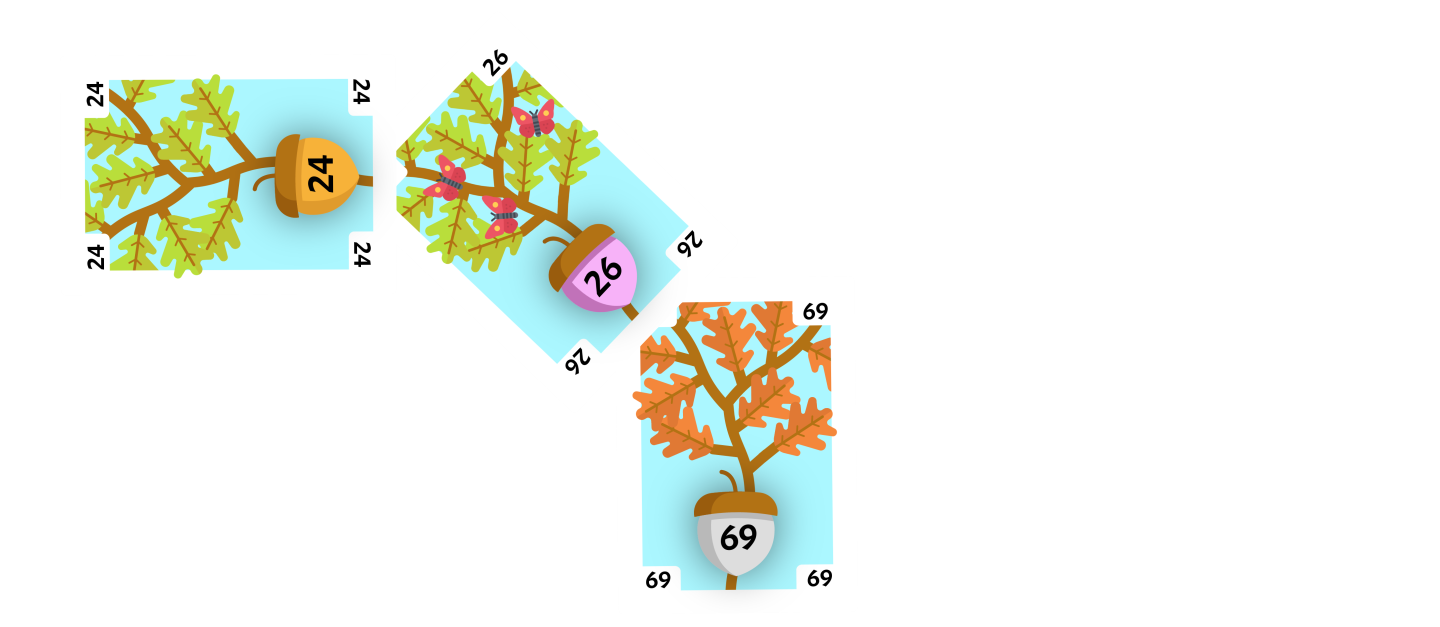
Add 24
The next card flipped up is the 24. We compare it to the root and determine that it is less than the root, so we look at the upper-left corner.
We find the 26 in this corner, and this becomes our current card. We compare our original 24 to the current card and determine that it is less than the current card, so we look at the upper-left corner.
There is no card in this corner, so we can place the card on this corner.
Since the flipped card 24 and the parent of the flipped card 26 are both left children, we will perform a Zig-Zig operation.
Since the parent card 26 is a left child, we will perform a right rotation with the parent card as our current card. The parent of our current card 69 will be our rotate card.
The rotate card will replace the right child of the current card. The current card had no right child so the rotation is finished.
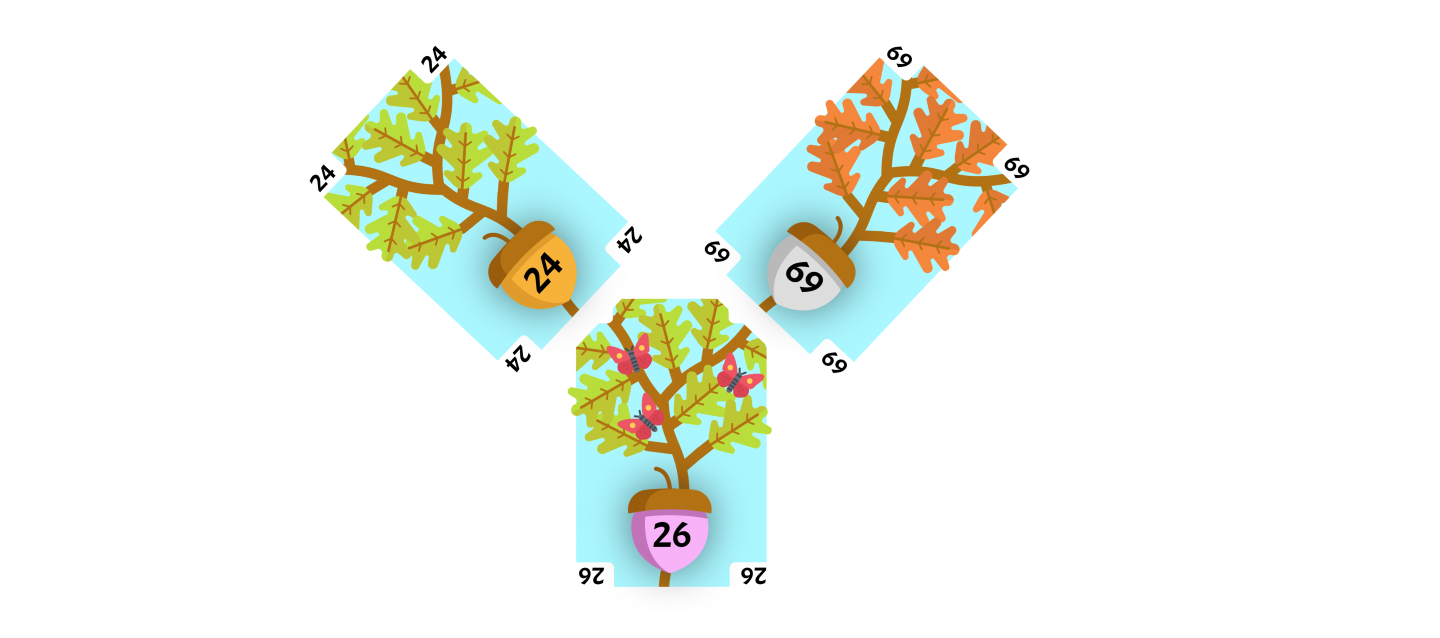
Since the flipped card 24 is a left child, we will perform a right rotation with the flipped card as our current card. The parent of our current card 26 will be our rotate card.
The rotate card will replace the right child of the current card. The current card had no right child so the rotation is finished. The flipped card 24 is now the root of the tree and we do not need to Splay again.
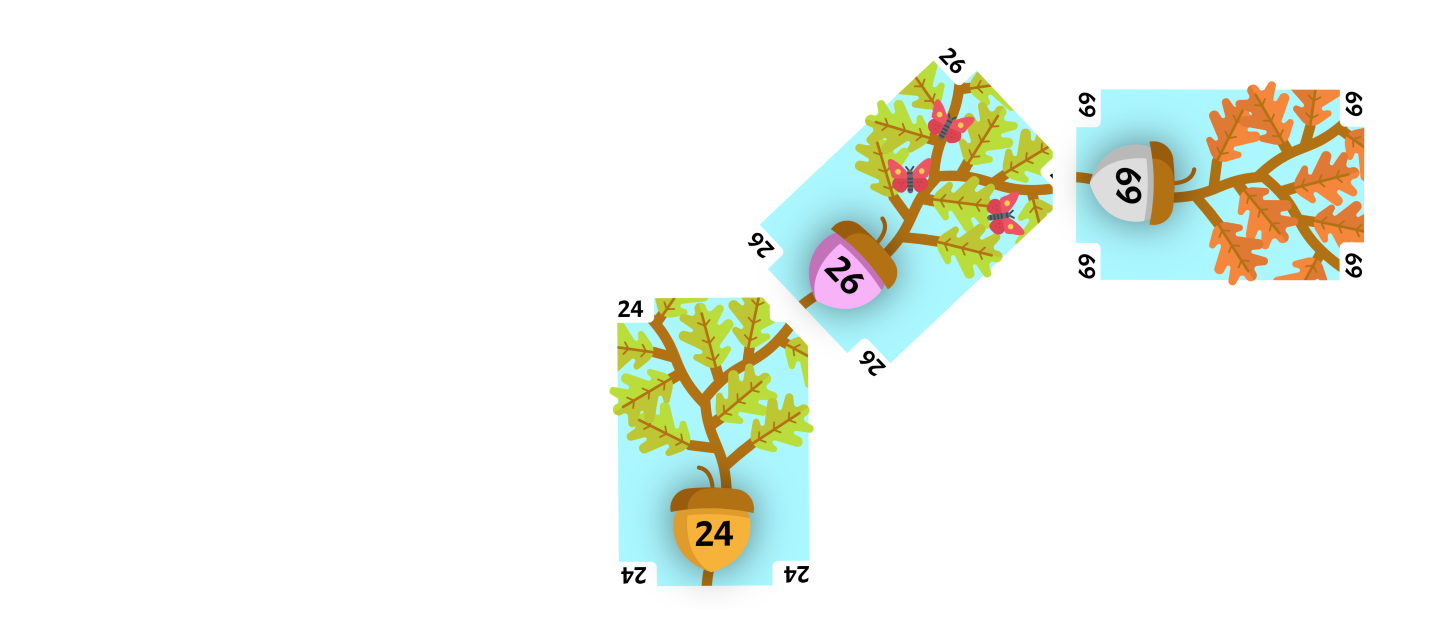
Add 5
The next card flipped up is the 5. We compare it to the root and determine that it is less than the root, so we look at the upper-left corner.
There is no card in this corner, so we can place the card on this corner.
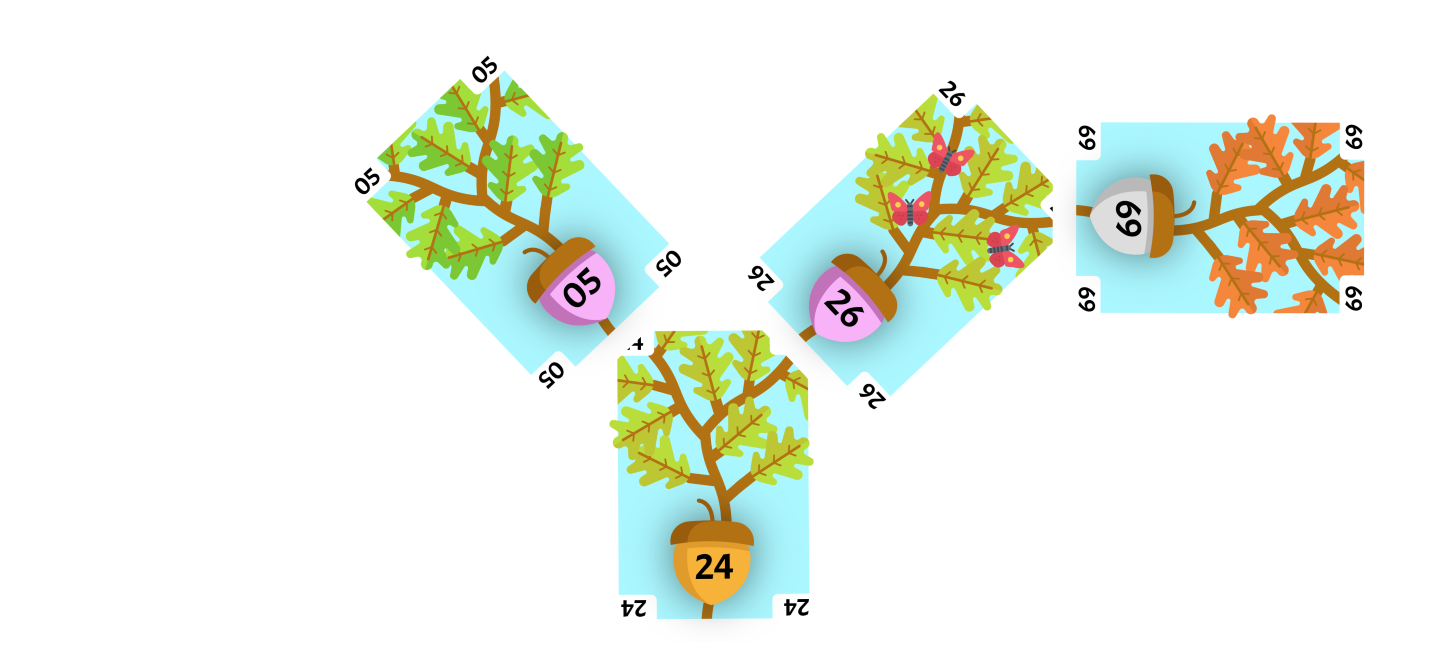
Since the flipped card 5 is a child of the root card we will perform a Zig operation. Since the flipped card is the left child of the root card, we will perform a right rotation with the flipped card as our current card. The parent of our flipped card, 24 will be our rotate card.
The rotate card will replace the right child of the current card. The current card had no right child so the rotation is finished. The flipped card 5 is now the root of the tree and we do not need to Splay again.
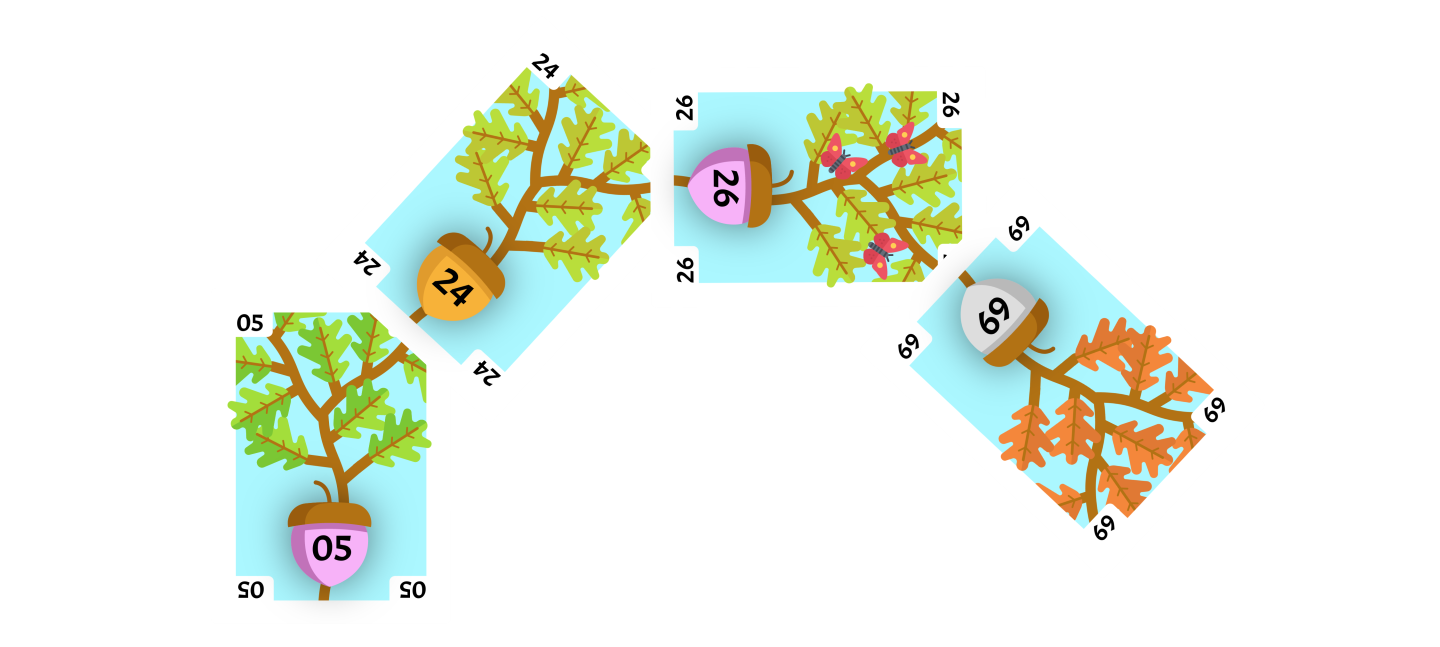
Add 19
The next card flipped up is the 19. We compare it to the root and determine that it is greater than the root, so we look at the upper-right corner.
We find the 24 in this corner, and this becomes our current card. We compare our original 19 to the current card and determine that it is less than the current card, so we look at the upper-left corner.
There is no card in this corner, so we can place the card on this corner.
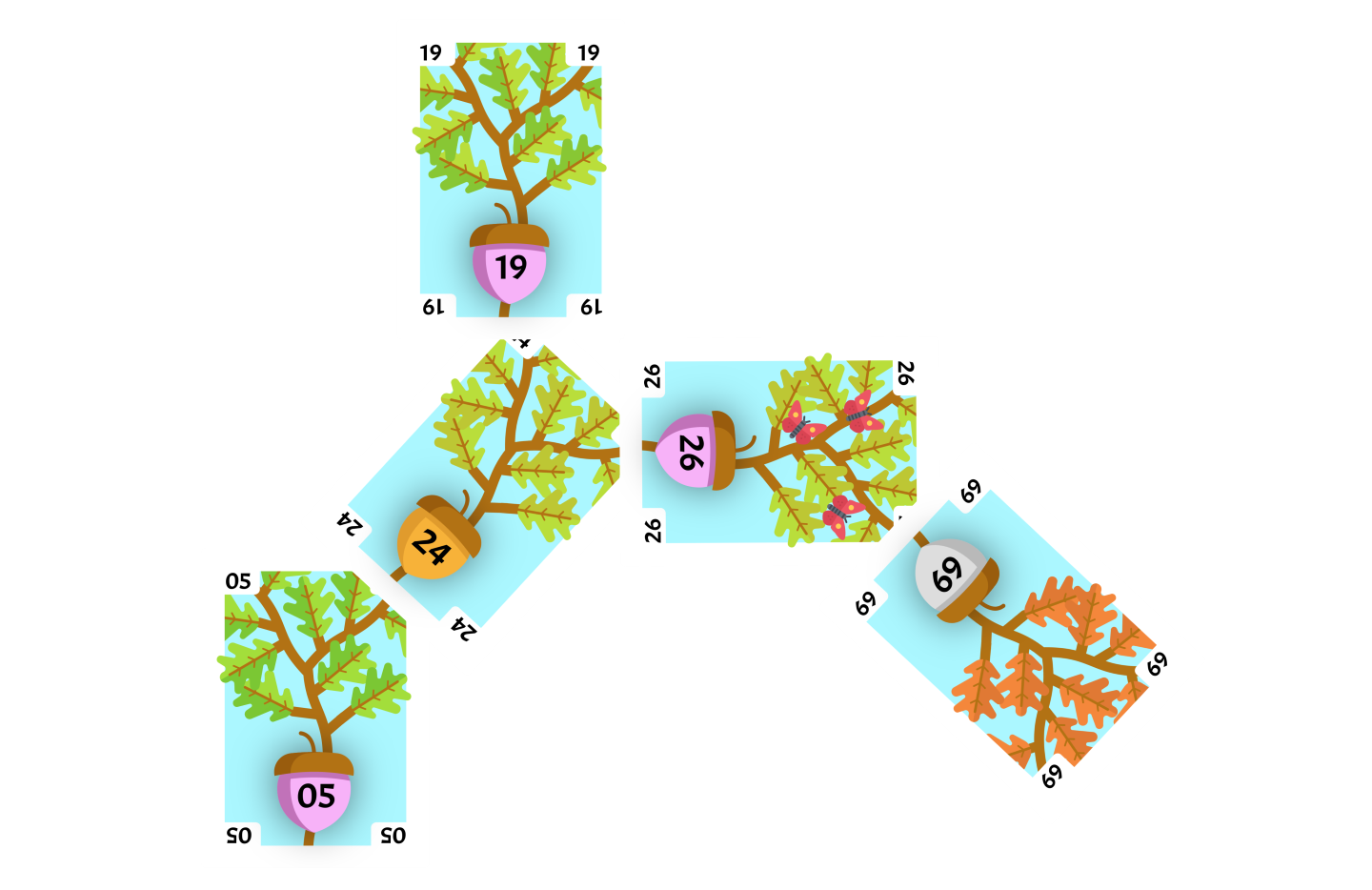
Since the flipped card 19 and the parent of the flipped card 24 are opposite children, we will perform a Zig-Zag operation.
Since the flipped card 19 is a left child, we will perform a right rotation with the flipped card as our current card. The parent of our current card, 24 will be our rotate card.
The rotate card will replace the right child of the current card. Since this rotation was done on a subtree, the current card will be placed where the rotate card used to be. The current card had no right child so the rotation is finished.
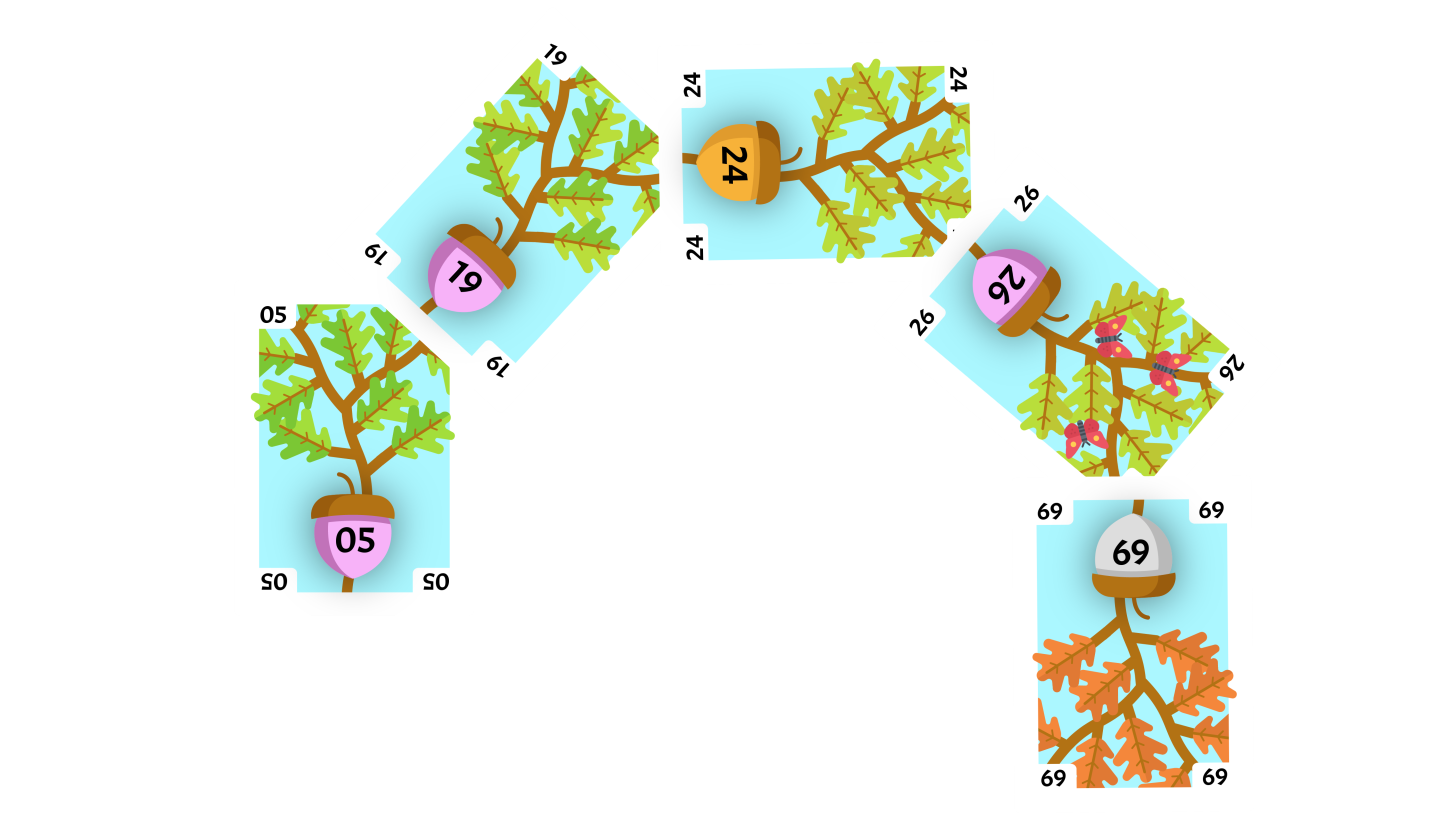
We will perform a left rotation with the flipped card as our current card. The parent of our current card, 05 will be our rotate card.
The rotate card will replace the left child of the current card. The current card had no left child so the rotation is finished. The flipped card 19 is now the root of the tree and we do not need to Splay again.
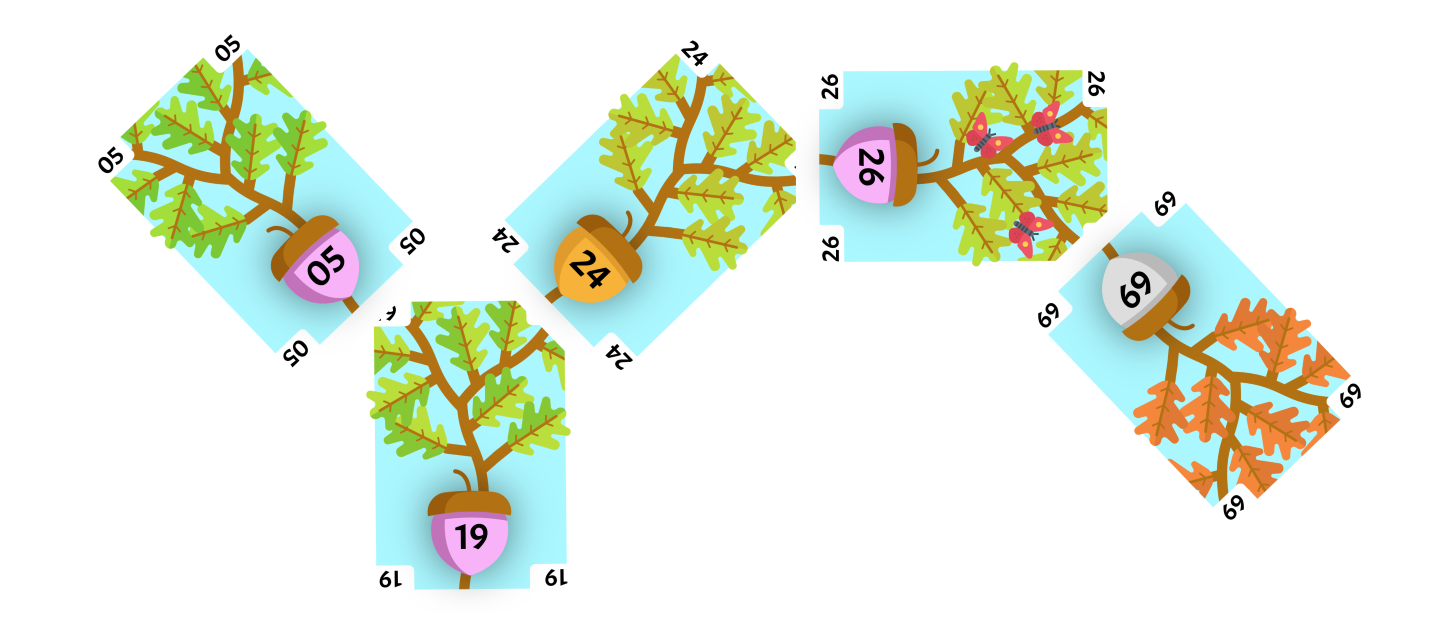
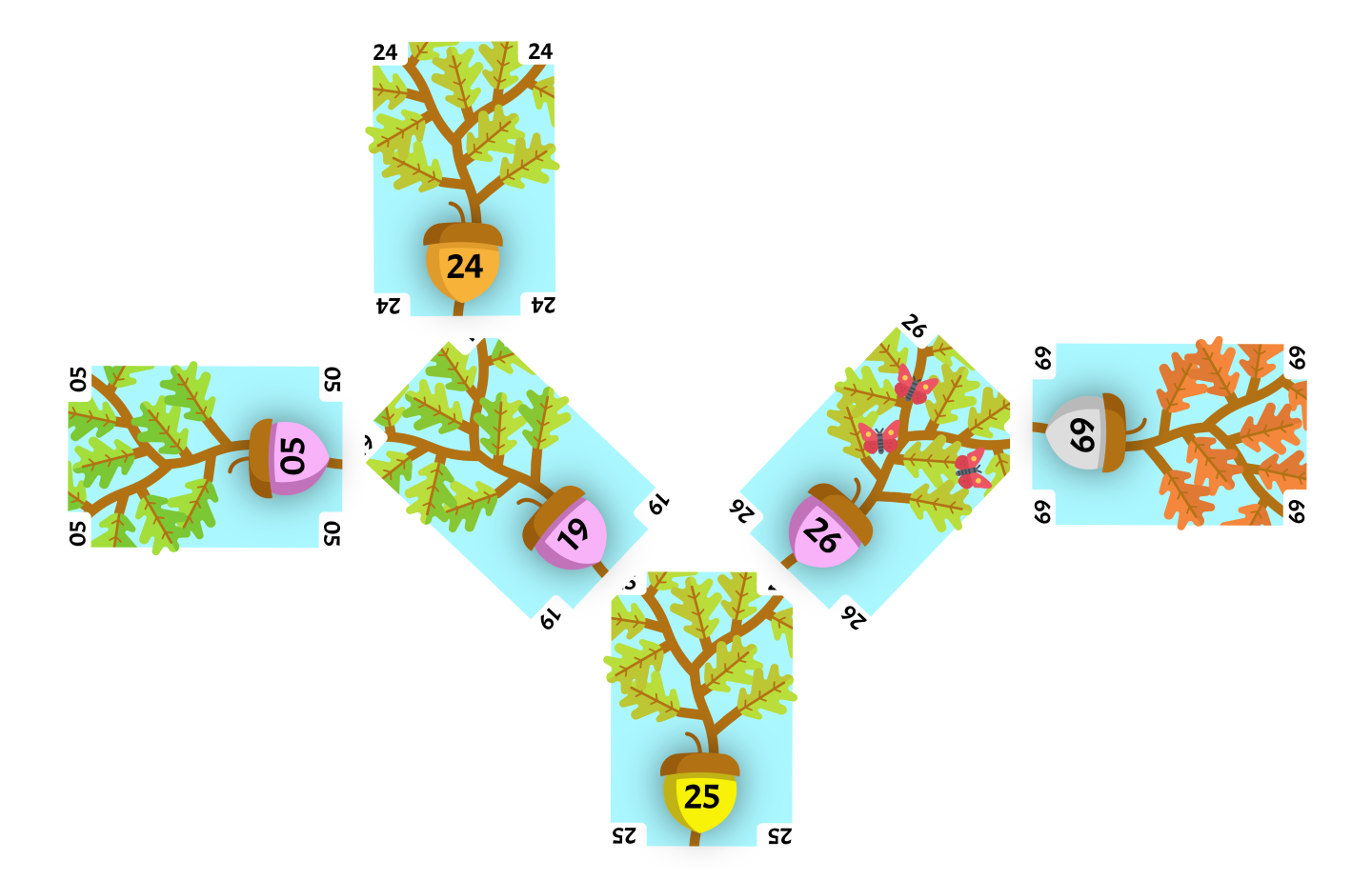
Add 25
The next card flipped up is the 25. We compare it to the root and determine that it is greater than the root, so we look at the upper-right corner.
We find the 24 in this corner, and this becomes our current card. We compare our original 25 to the current card and determine that it is greater than the current card, so we look at the upper-right corner.
We find the 26 in this corner, and this becomes our current card. We compare our original 25 to the current card and determine that it is less than the current card, so we look at the upper-left corner.
There is no card in this corner, so we can place the card on this corner.
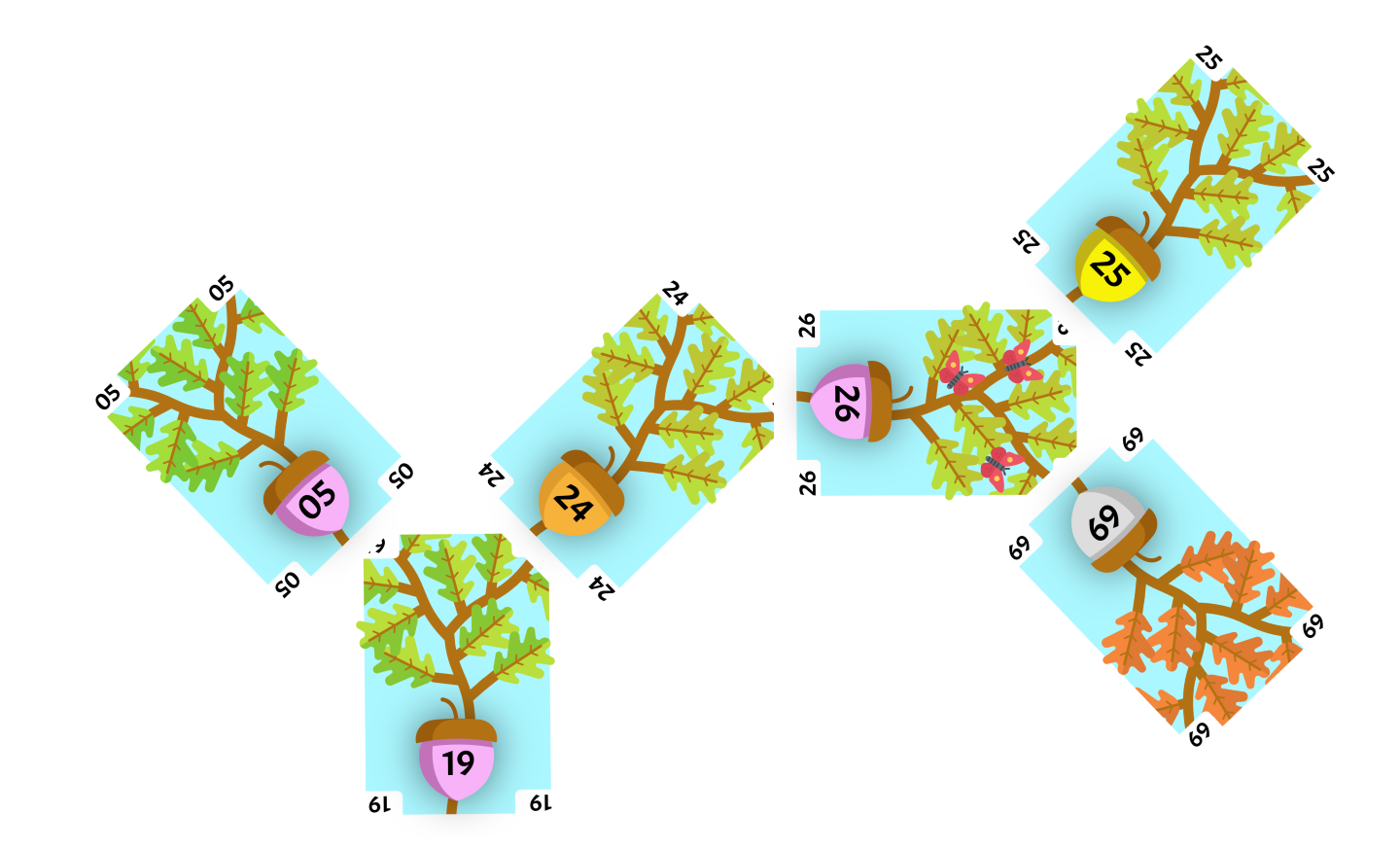
Since the flipped card 25 and the parent of the flipped card 26 are opposite children, we will perform a Zig-Zag operation.
Since the flipped card 25 is a left child, we will perform a right rotation with the flipped card as our current card. The parent of our current card, 26 will be our rotate card.
The rotate card will replace the right child of the current card. Since this rotation was done on a subtree, the current card will be placed where the rotate card used to be. The current card had no right child so the rotation is finished.
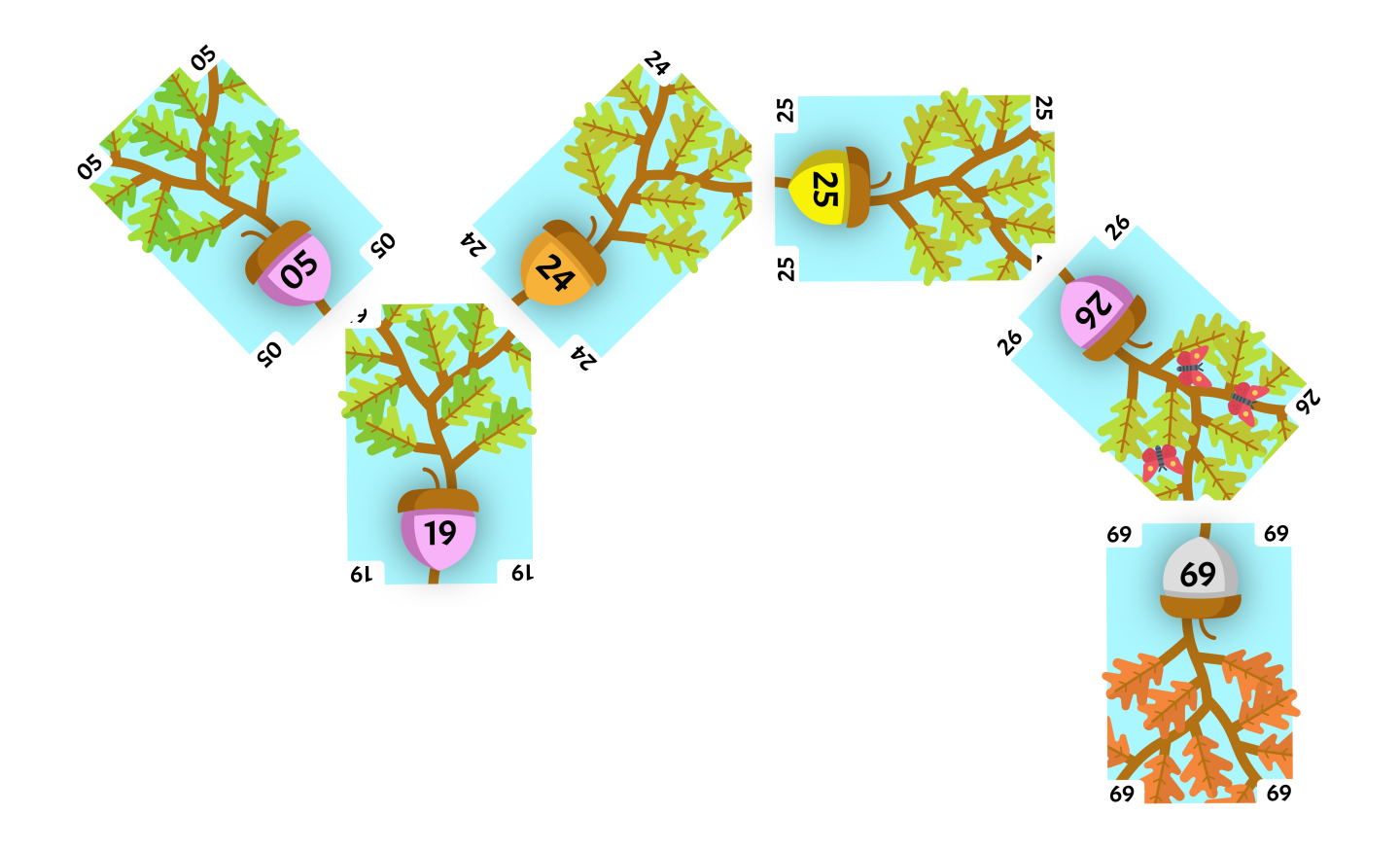
We will perform a left rotation with the flipped card as our current card. The parent of our current card, 24 will be our rotate card.
The rotate card will replace the left child of the current card. Since this rotation was done on a subtree, the current card will be placed where the rotate card used to be. The current card had no left child so the rotation is finished. The flipped card 25 is not the root of the tree and we need to Splay again.
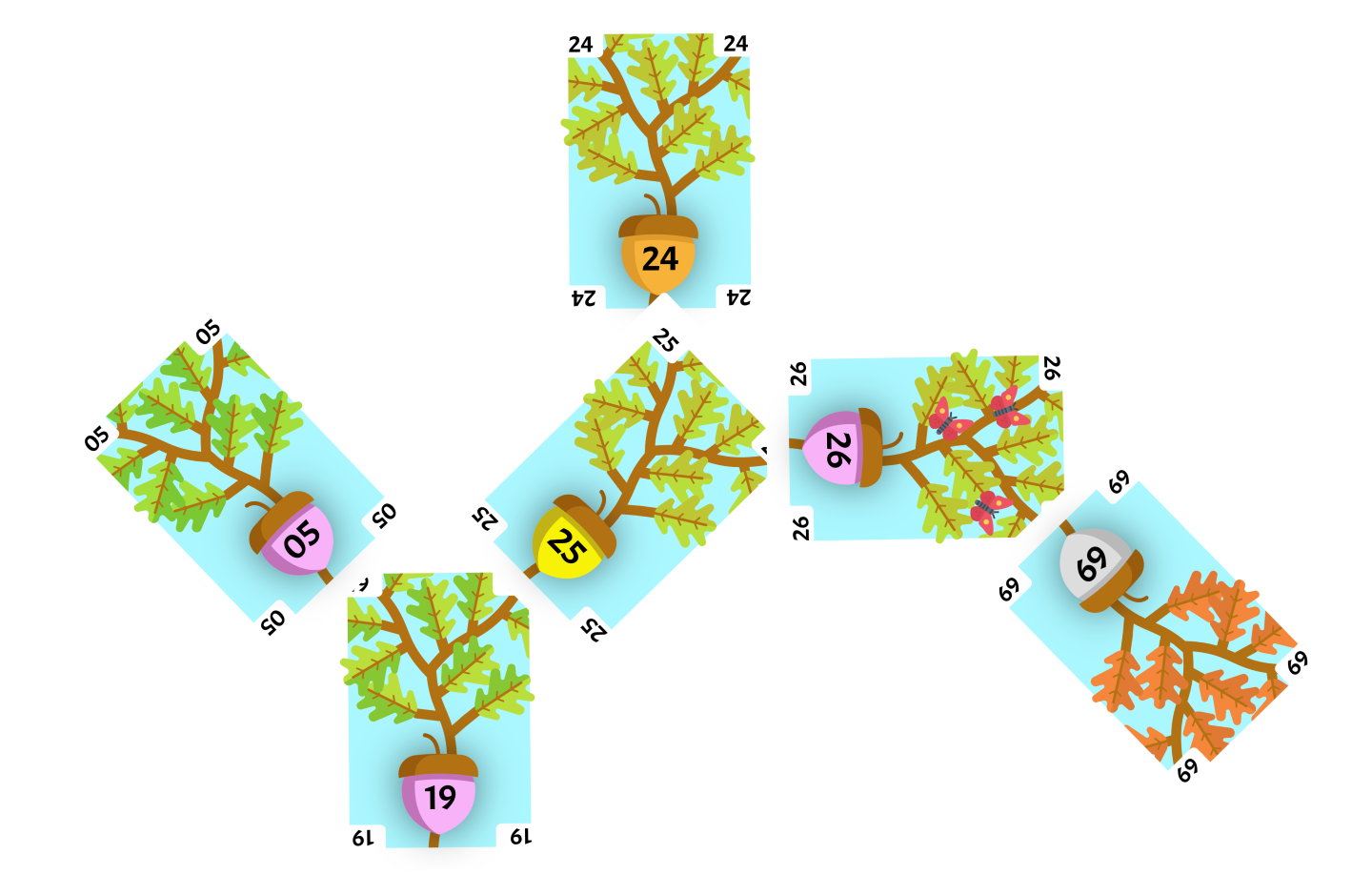
Since the flipped card 25 is a child of the root card we will perform a Zig operation. Since the flipped card is the right child of the root card, we will perform a left rotation with the flipped card as our current card. The parent of our current card 19 will be our rotate card.
The rotate card will replace the left child of the current card. The current card’s left child that was replaced will be the right child of the rotate card. The flipped card 25 is now the root of the tree and we do not need to Splay again.