Binary Search Tree Rotation Algorithm
Goals
Students will understand elements of the rotation algorithm for binary search trees.
Video
Materials
One deck of Acorn cards.

Setup
Shuffle the deck and deal each student 9 cards.
Each student will shuffle their 9 cards, and then create a binary tree as demonstrated on the insertion algorithm page.
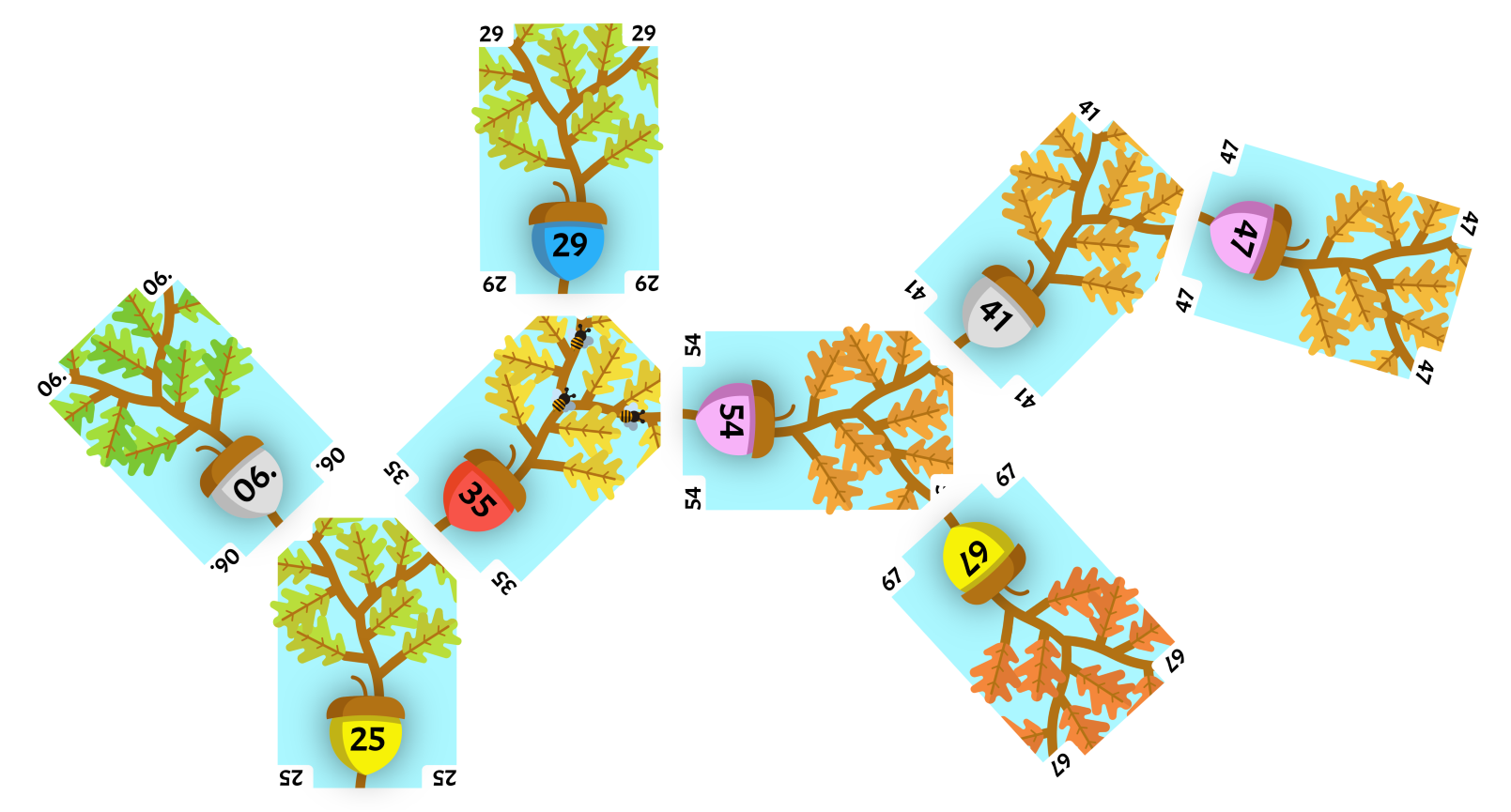
Algorithm
The card chosen to be rotated is our root card. The child of the root card on the opposite side of rotation is the pivot card, ex. the left child for a right rotation.
-
Replace the side of rotation child of the pivot card with the root card. Keep all of the root card children on the side of rotation intact. Set aside the side of rotation child and keep all of the children intact.
-
Place the side of rotation child of the pivot card that was replaced in step 1 as the opposite side of rotation child of the root card.
Example
This is an example of a right-side rotation of the root 35 of our tree.
Since this is a right-side rotation, the left child of our root, 25 is the pivot card.
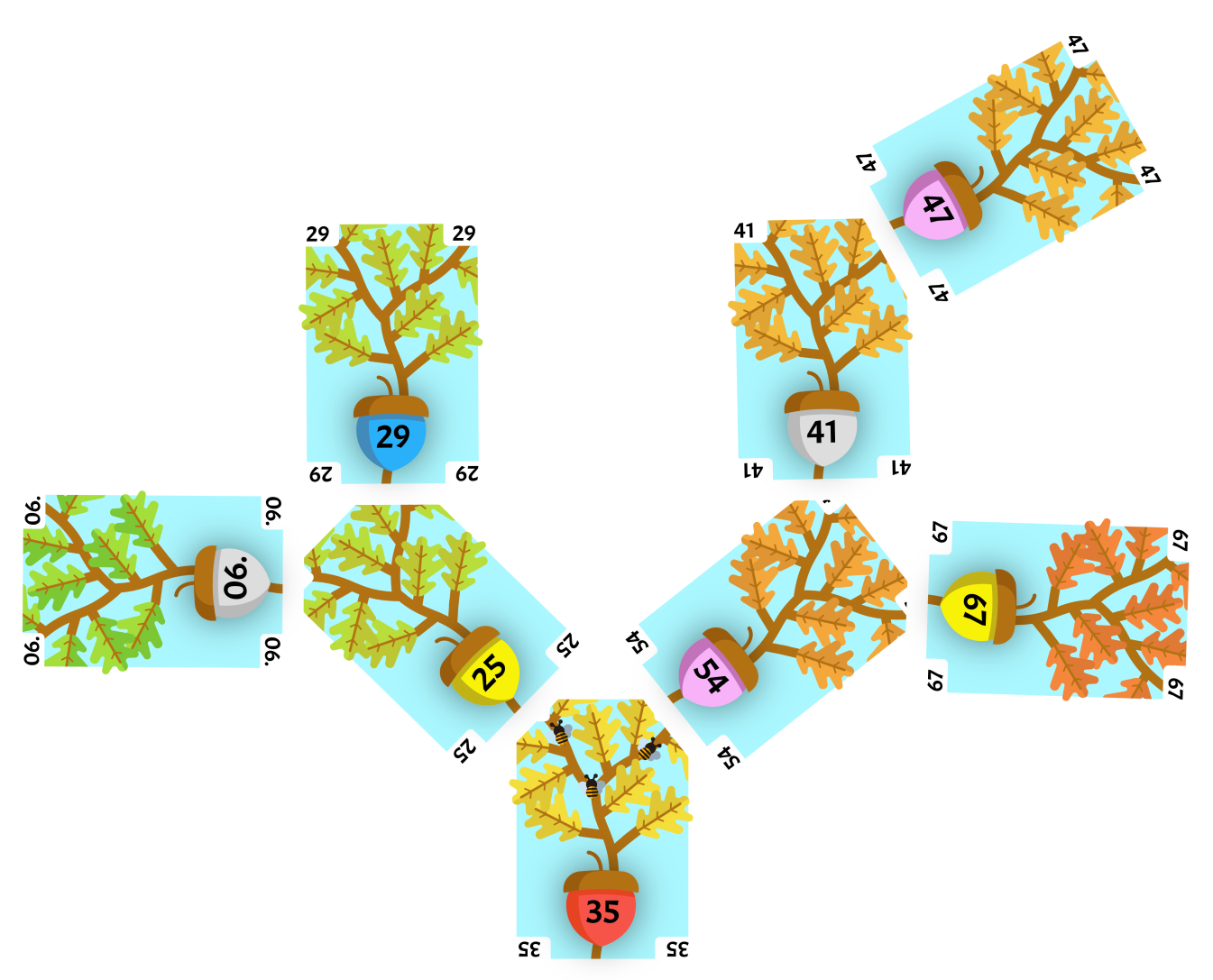
The side of rotation child 29 of the pivot card 25 is replaced by the root card 35, with all of the root card’s children intact. 29 has no children so only itself is set aside.
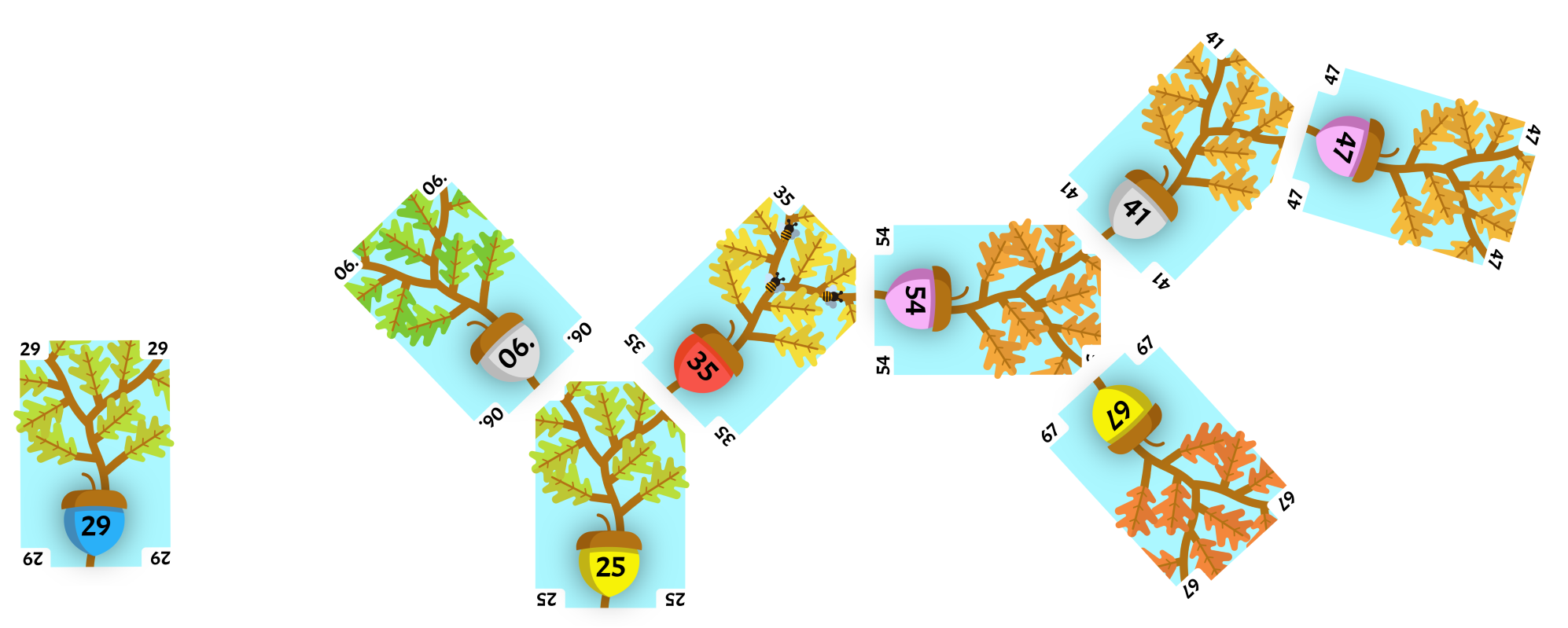
The side of rotation child 29 is placed as the opposite side of rotation child of the root card.