Binary Search Tree Removal Algorithm
Goals
Students will understand elements of the removal algorithm for binary search trees.
Video
Materials
One deck of Acorn cards.

Setup
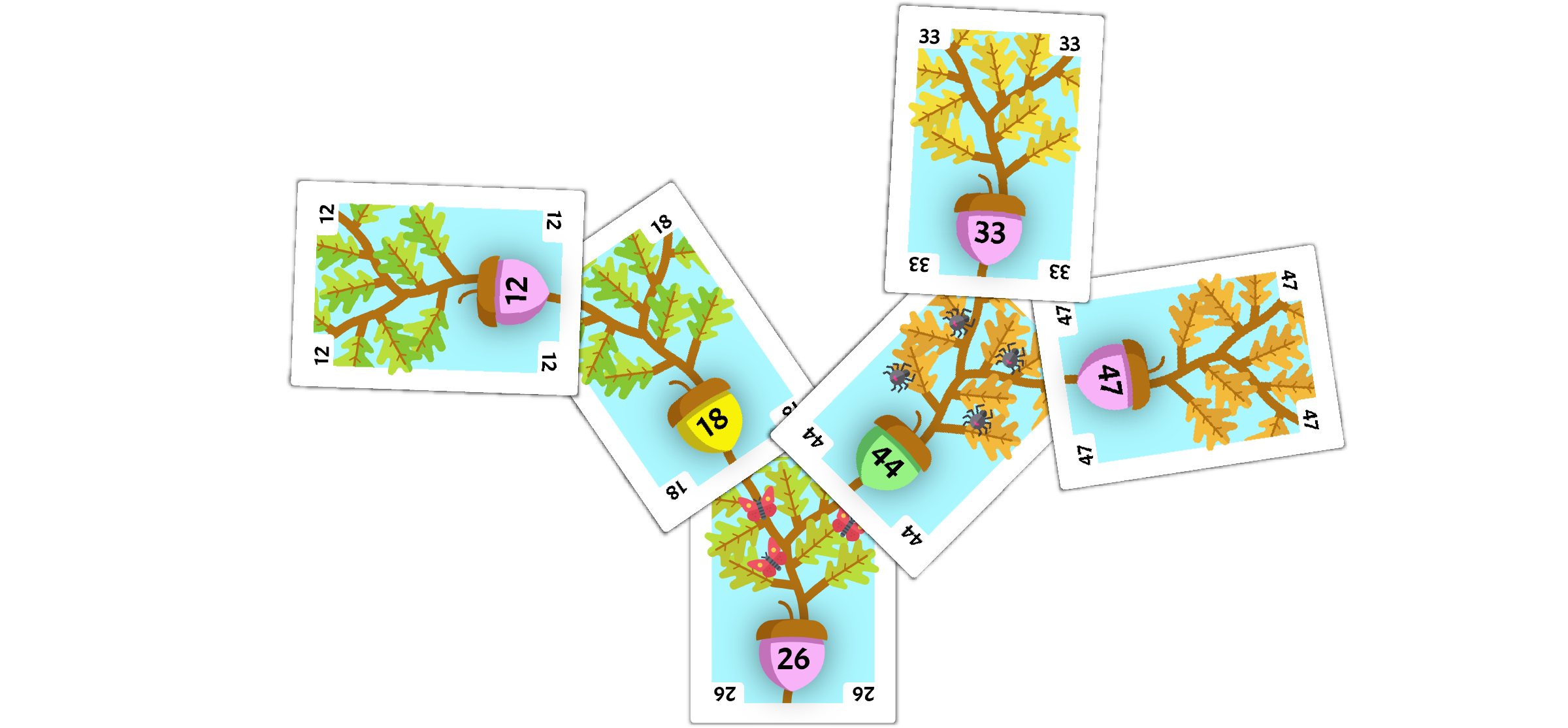
Shuffle the deck and deal each student 9 cards.
Each student will shuffle their 9 cards, and then create a binary tree as demonstrated on the insertion algorithm page.
Algorithm
There are three cases possible when removing a card from a binary search tree.
- The card is a leaf (no corners covered).
- The card is in the middle of the tree with only one corner covered.
- The card is in the middle of the tree with both corners covered.
Removing a leaf
When removing a leaf card at the edge of the tree, there are no consequences. Just remove the card.
Removing from the middle, one corner
When removing a card in the middle of the tree with only one corner covered, it will create a hole in your tree. Remove the card, then shift the branch back, covering the same corner as the removed did.
Removing from the middle, two corners
When removing a card in the middle of the tree with both corners covered, it will create a hole in your tree. To fix it, we will need to find the next-highest card in the tree.
-
First, look at the upper-right corner of the card to be removed. This card should be greater than the card to be removed. We will call this the possible card.
-
If the possible card has a card in the upper-left corner, then this new card becomes the possible card. Repeat this step until the upper-left corner is empty.
-
Once you find a card where the upper-left corner is empty, you have found the next-highest card. Take out the card to be removed from the tree, and replace it with the next-highest card.
-
Now, repair the tree the next-highest card, following this same algorithm. Note that the next-highest card is either a leaf or has only one corner covered, both of which involve simple fixes to the tree.
Example
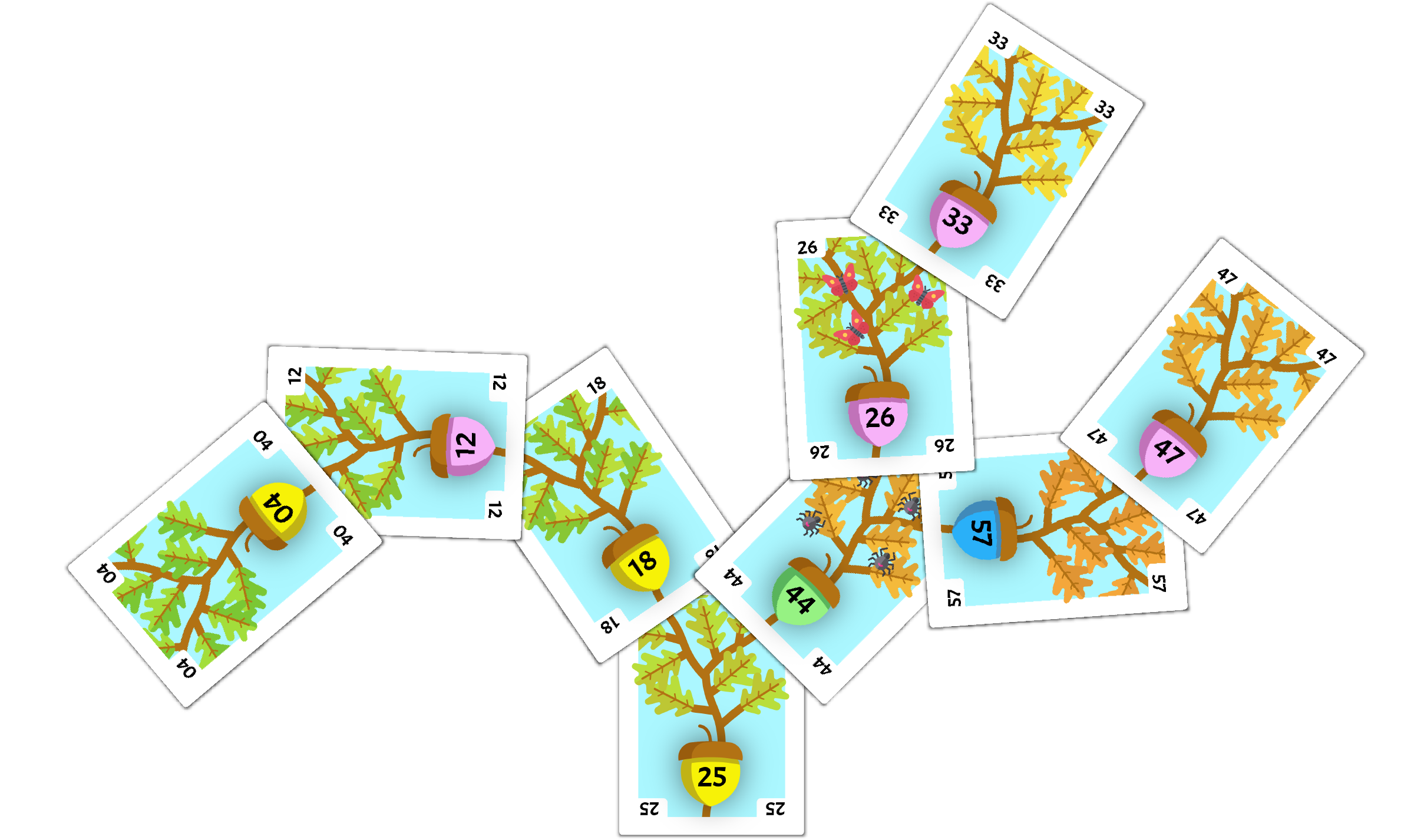
Remove 04
Our first card to remove from the tree is 04. This card is highlighted in the image below.
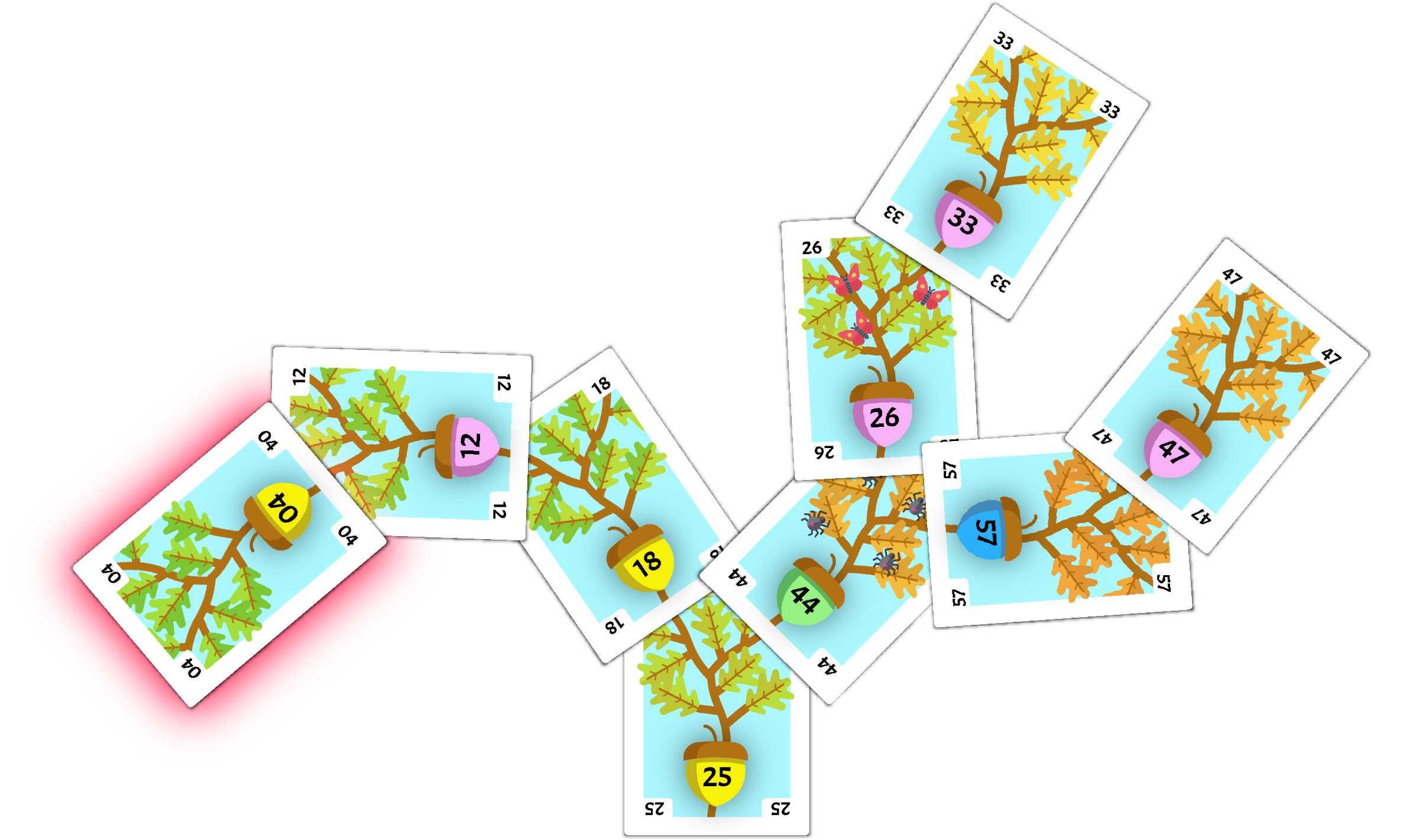
The 04 card is a leaf in our tree, so it can simply be removed without consequences, as shown below.
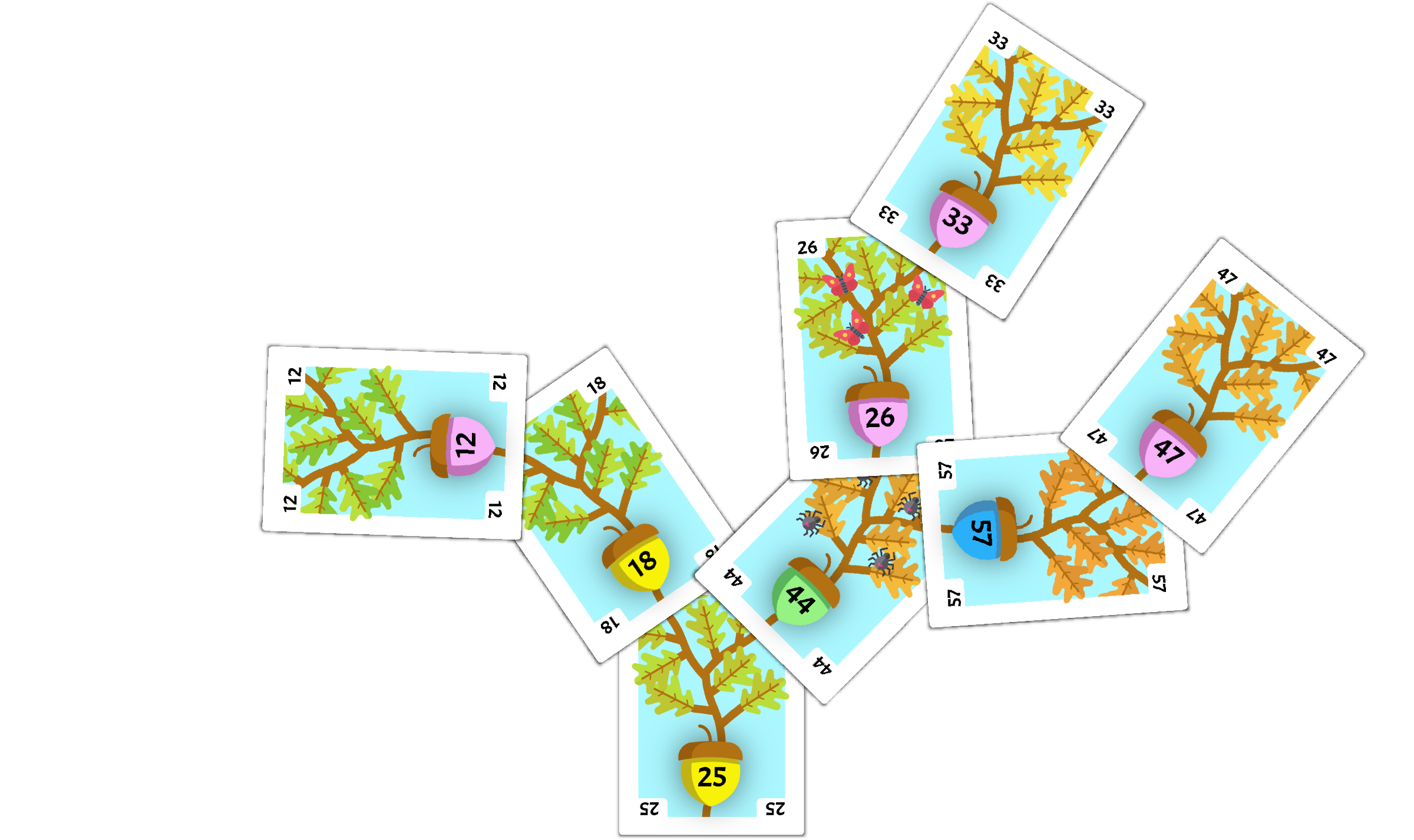
Remove 57
Next, we will remove the 57 card from the tree, highlighted below.
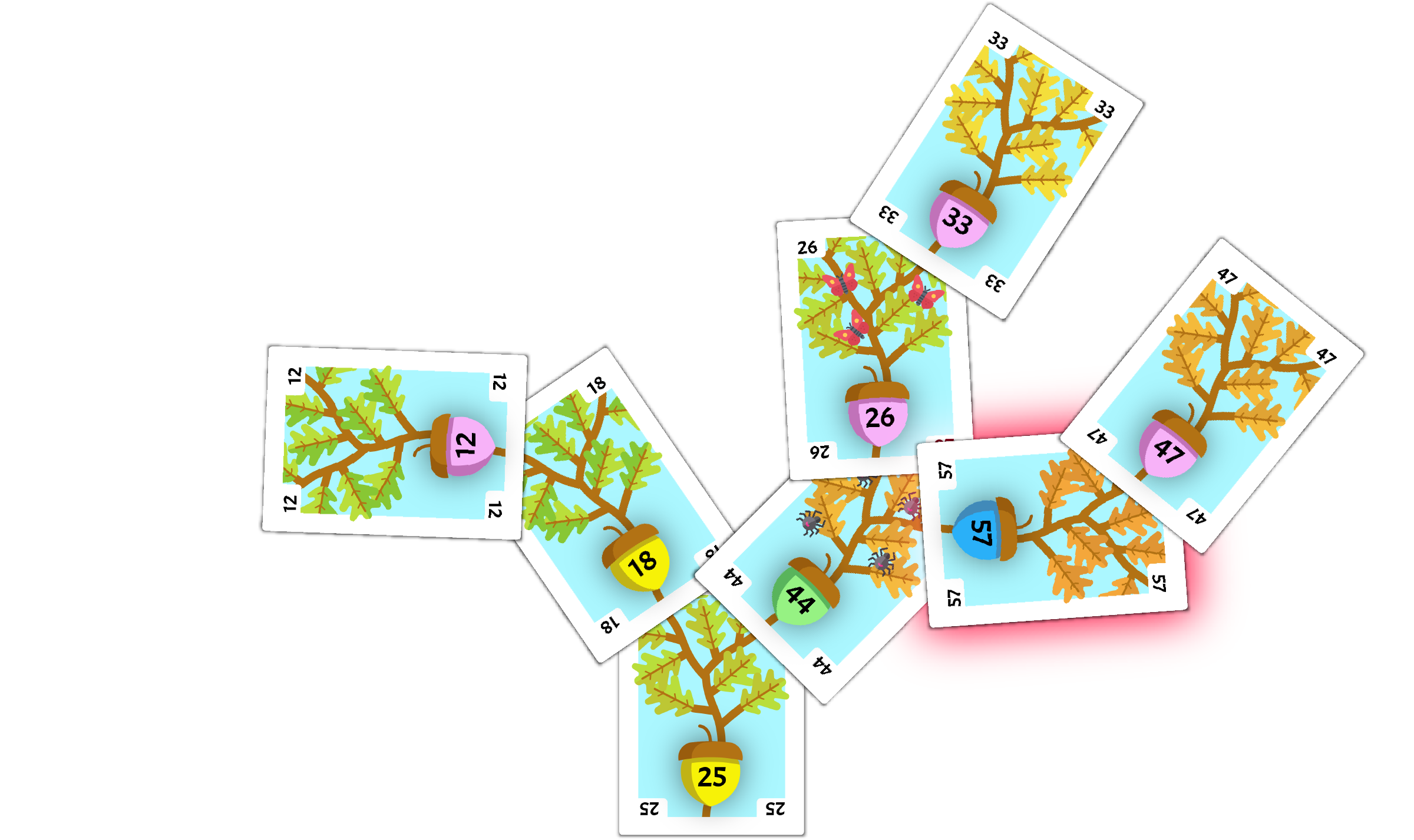
The 57 card is in the middle of the tree with one corner covered. This means we can remove the card, and then shift the following cards back to take its place, as shown below.
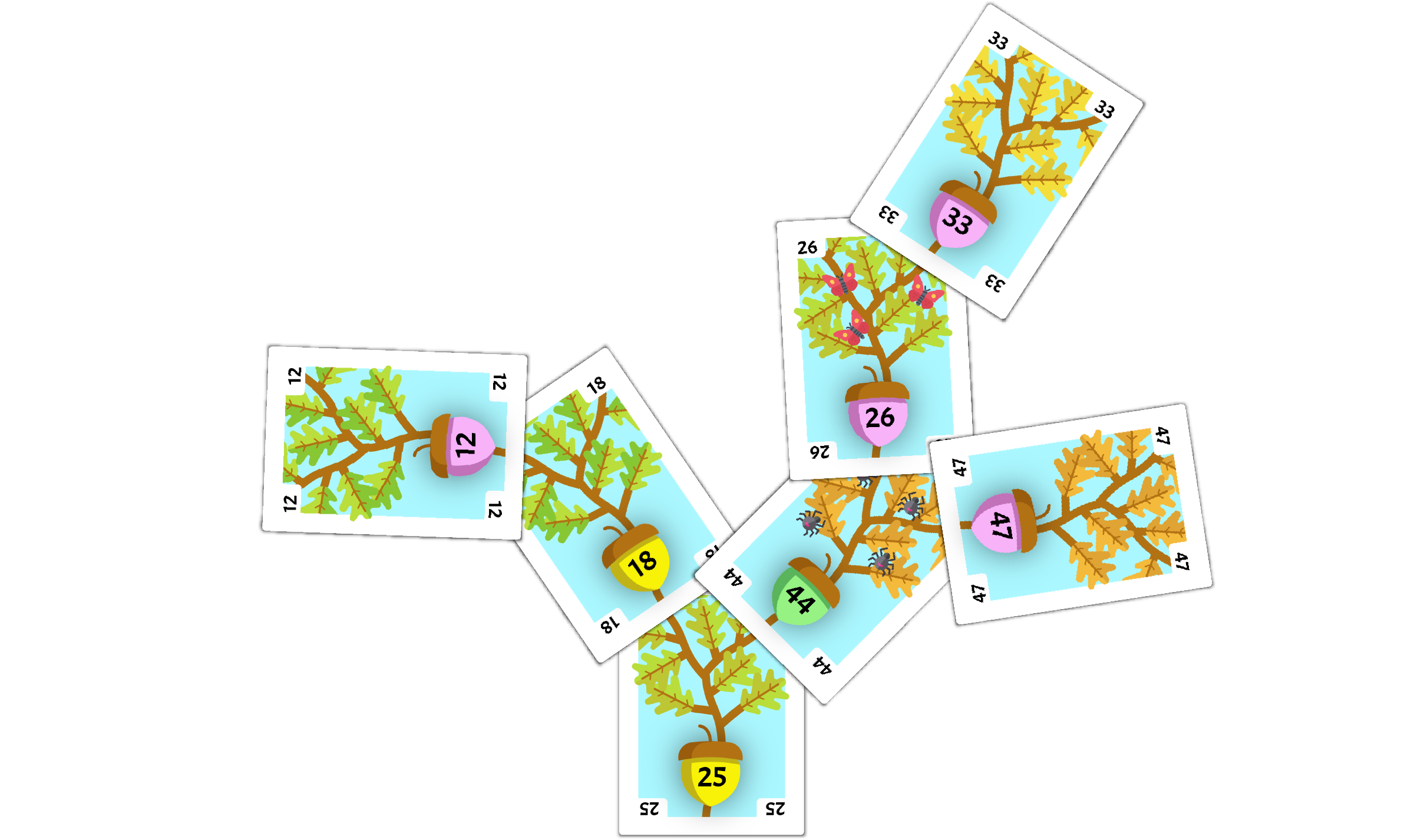
Remove 25
Finally, we remove the 25 card, which is the root of the tree. This card is highlighted below.

Since this card is in the middle of the tree with two corners covered, we need to find the next-highest card in the tree. This is the 26 card, highlighted below in green. We find the 26 by first looking at the upper-right corner of the 25 card, then repeatedly looking in the upper-left corner of each subsequent card until this corner is empty.

To complete the removal, we replace the 25 card with the 26 card, then resolve the removal of the 26. Since the 26 card had only one corner covered, we can shift the following cards back to take its place, as shown below.