Huffman Coding Algorithm
Goals
Students will understand elements of the Huffman coding algorithm, which assigns weights to the corresponding frequency of a letter in a sentence in order to build a binary search tree.
Video
Materials
One deck of Acorn cards.

Eight letter chits per student.
Setup
Shuffle the deck and deal each student 8 cards. Give each student 8 random chits.
Each student will place their 8 cards in a row face-up to form a collection in front of you. Each student will place a chit on each face-up card and then sort the collection
Whenever we sort the collection, you are free to use whichever sorting method you have previously learned.
Algorithm
Constructing the Tree
-
Sort the collection and remove the two least-valued cards from the collection. Draw a card from the deck and place it face-down as the root card of a new subtree. Place the least-value of the two cards as the left child of the root card and the greatest-value as the right child. The face-down root card has the value of its children added together. Reinsert the root card into the collection keeping all of its children intact and sort the collection.
-
If there is more than one card in the collection, repeat step 1.
Assigning a Binary Value
For each leaf of the tree, a new binary value can be assigned to it based on the route to the leaf from the root. For each Binary value, our current card is the root of the tree.
-
If the current card is the leaf we are looking for, we assign the binary value to it.
-
If the next card in the path to the leaf is the left child of the current card, the next binary number in the binary value is 0. The left child is the new current card.
-
If the next card in the path to the leaf is the right child of the current card, the next binary number is 1. The right child is the new current card.
Example
First we lay out our initial collection, place a chit on each card, and then sort the collection.

Constructing the Tree
We will remove the two least-valued cards 10 and 17 from our collection. We will draw a card from the deck and place it face-down as the root of a new subtree. 10 is the least-value of the two cards we removed so it will be the left child of the root card. 17 is the greatest-value of the two cards we removed so it will be the right child of the root card. The value of the face-down card is 27, we will reinsert it into the collection with all of it’s children intact and sort the collection. There are 7 cards in the collection, so we will have to repeat this step.
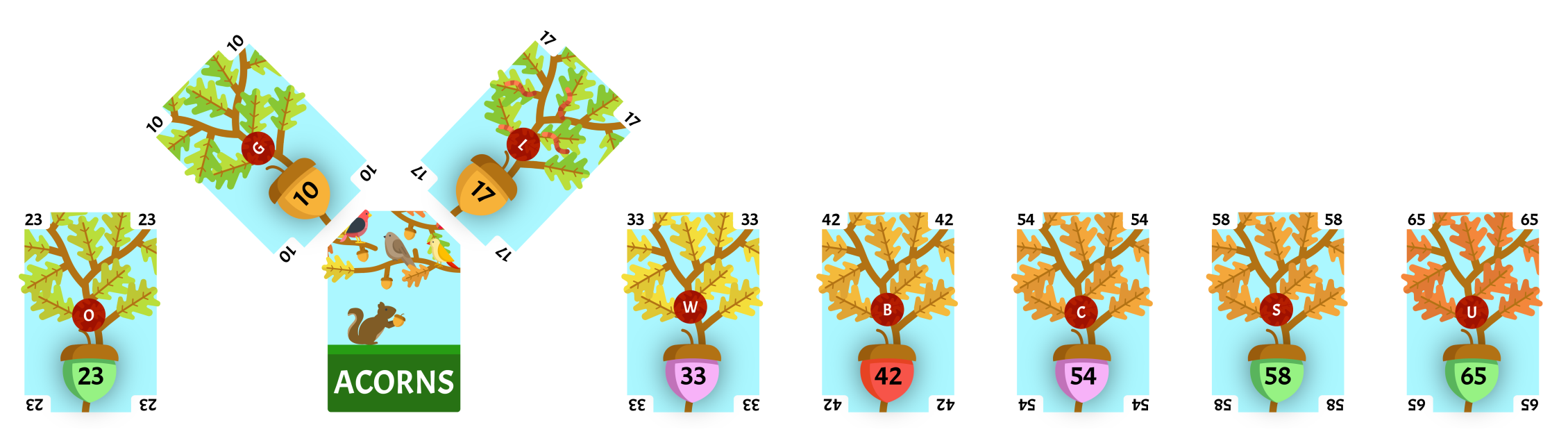
We will remove the two least-valued cards 23 and our face-down card with a value of 27 from our collection. We will draw a card from the deck and place it face-down as the root of a new subtree. 23 is the least-value of the two cards we removed so it will be the left child of the root card. 27 is the greatest-value of the two cards we removed so it will be the right child of the root card. The value of the face-down card is 50, we will reinsert it into the collection with all of it’s children intact and sort the collection. There are 6 cards in the collection, so we will have to repeat this step.
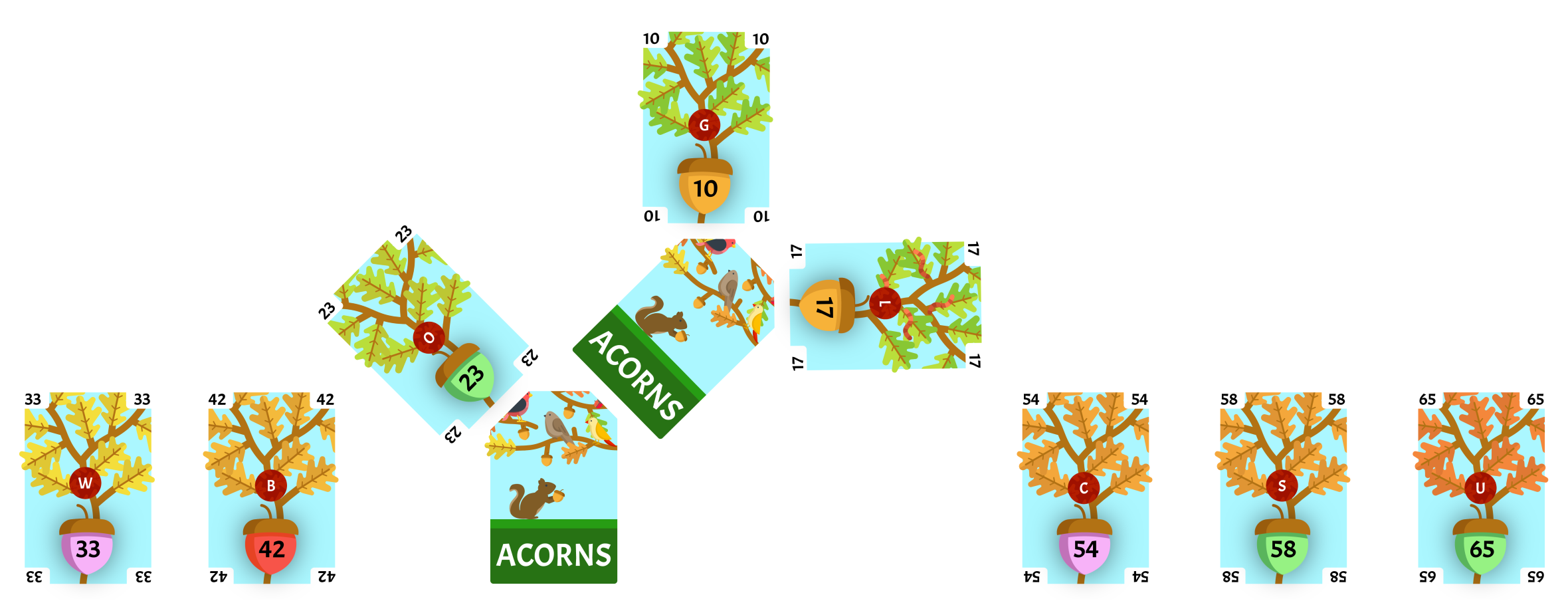
We will remove the two least-valued cards 33 and 42 from our collection. We will draw a card from the deck and place it face-down as the root of a new subtree. 33 is the least-value of the two cards we removed so it will be the left child of the root card. 42 is the greatest-value of the two cards we removed so it will be the right child of the root card. The value of the face-down card is 72, we will reinsert it into the collection with all of it’s children intact and sort the collection. There are 5 cards in the collection, so we will have to repeat this step.
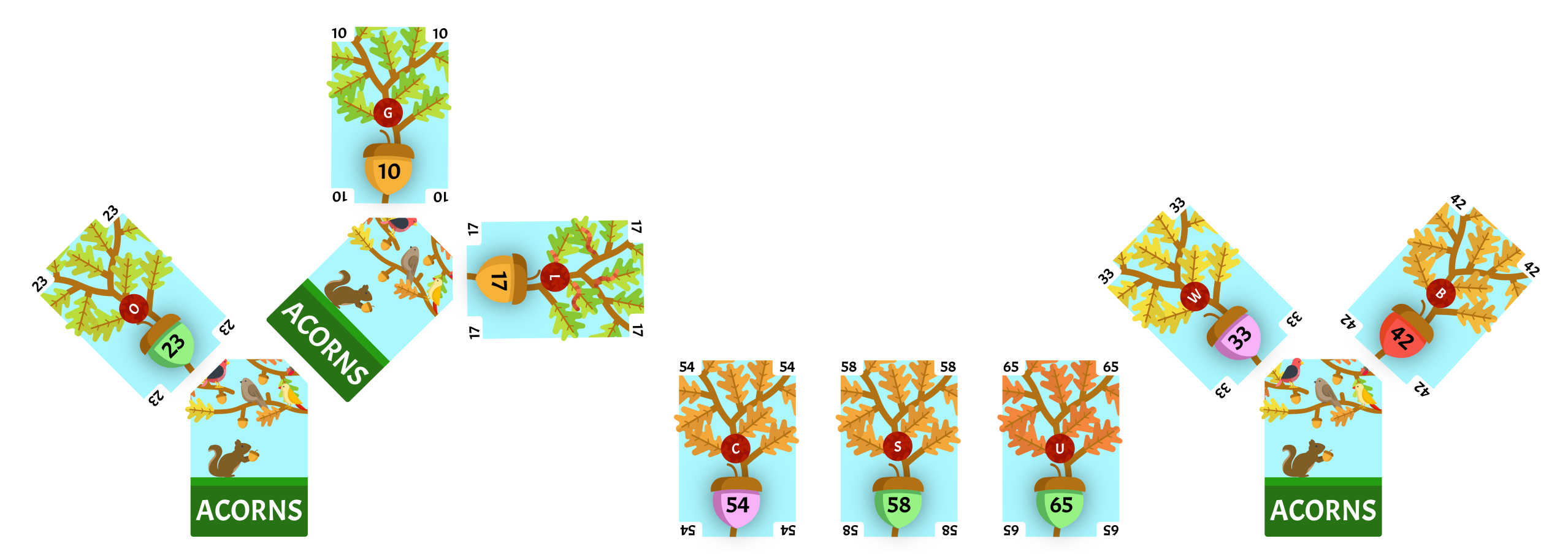
We will remove the two least-valued cards 54 and our face-down card with a value of 50 from our collection. We will draw a card from the deck and place it face-down as the root of a new subtree. 50 is the least-value of the two cards we removed so it will be the left child of the root card. 54 is the greatest-value of the two cards we removed so it will be the right child of the root card. The value of the face-down card is 104, we will reinsert it into the collection with all of it’s children intact and sort the collection. There are 4 cards in the collection, so we will have to repeat this step.
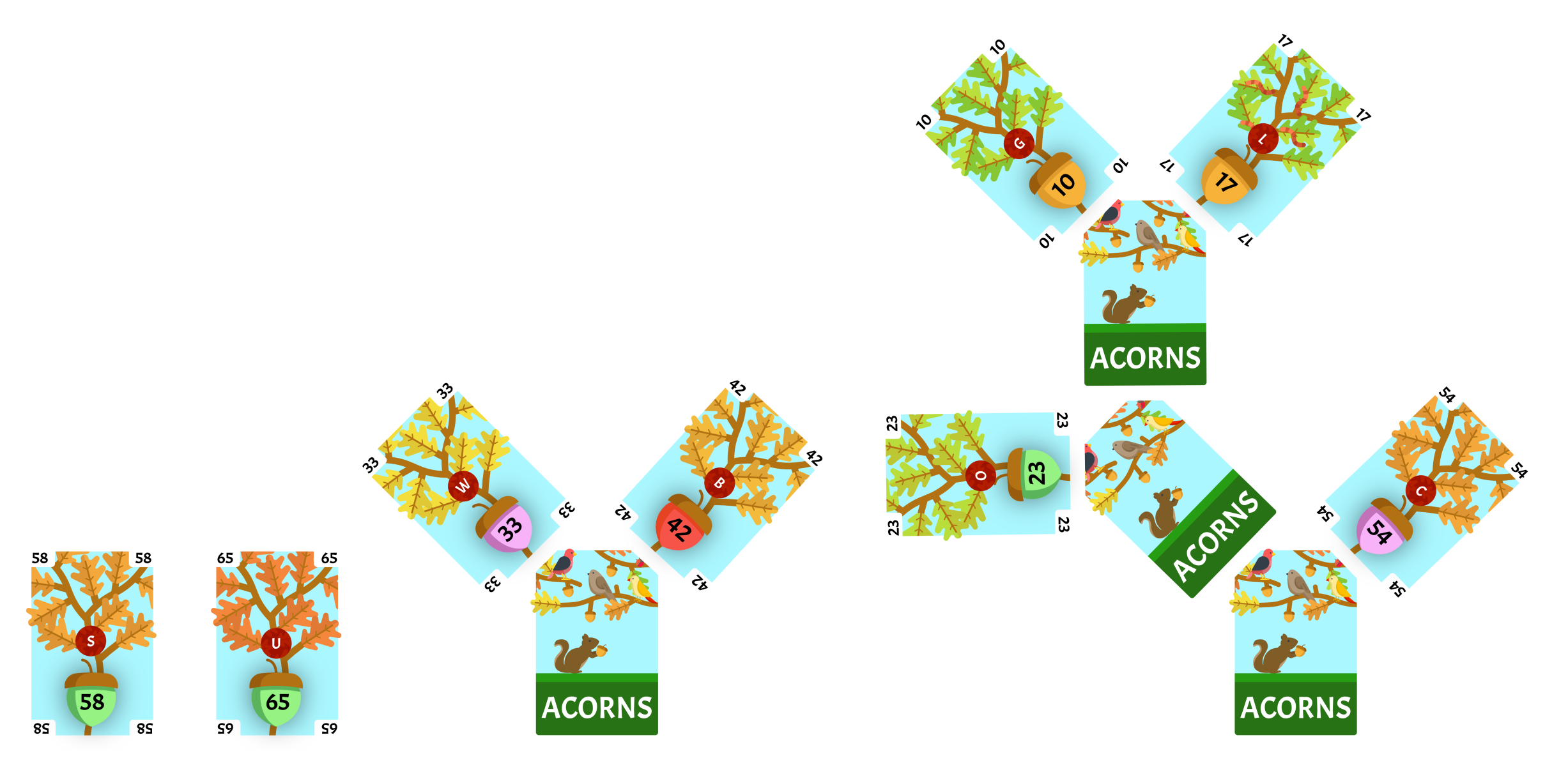
We will remove the two least-valued cards 58 and 65 from our collection. We will draw a card from the deck and place it face-down as the root of a new subtree. 58 is the least-value of the two cards we removed so it will be the left child of the root card. 65 is the greatest-value of the two cards we removed so it will be the right child of the root card. The value of the face-down card is 123, we will reinsert it into the collection with all of it’s children intact and sort the collection. There are 3 cards in the collection, so we will have to repeat this step.
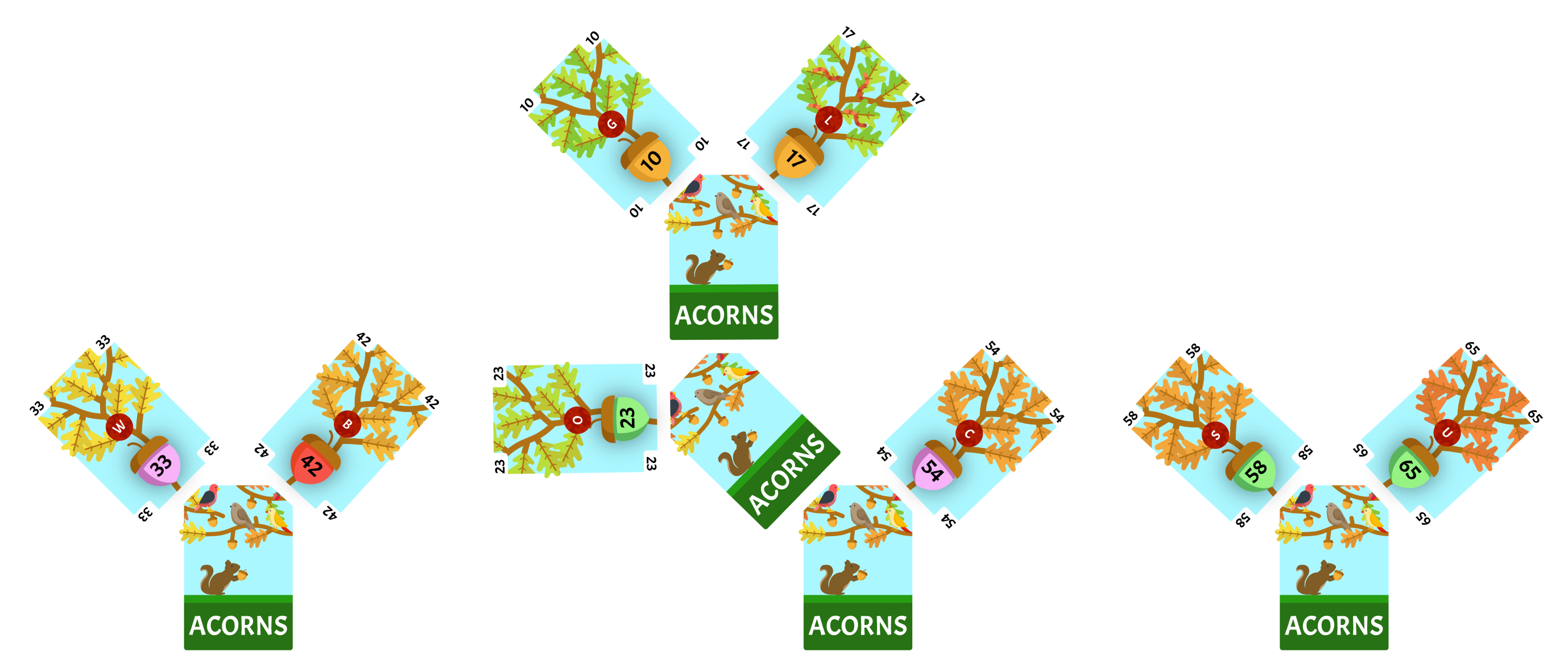
We will remove the two least-valued cards, our face-down card with a value of 72 and our face-down card with a value of 104, from our collection. We will draw a card from the deck and place it face-down as the root of a new subtree. 72 is the least-value of the two cards we removed so it will be the left child of the root card. 104 is the greatest-value of the two cards we removed so it will be the right child of the root card. The value of the face-down card is 176, we will reinsert it into the collection with all of it’s children intact and sort the collection. There are 2 cards in the collection, so we will have to repeat this step.
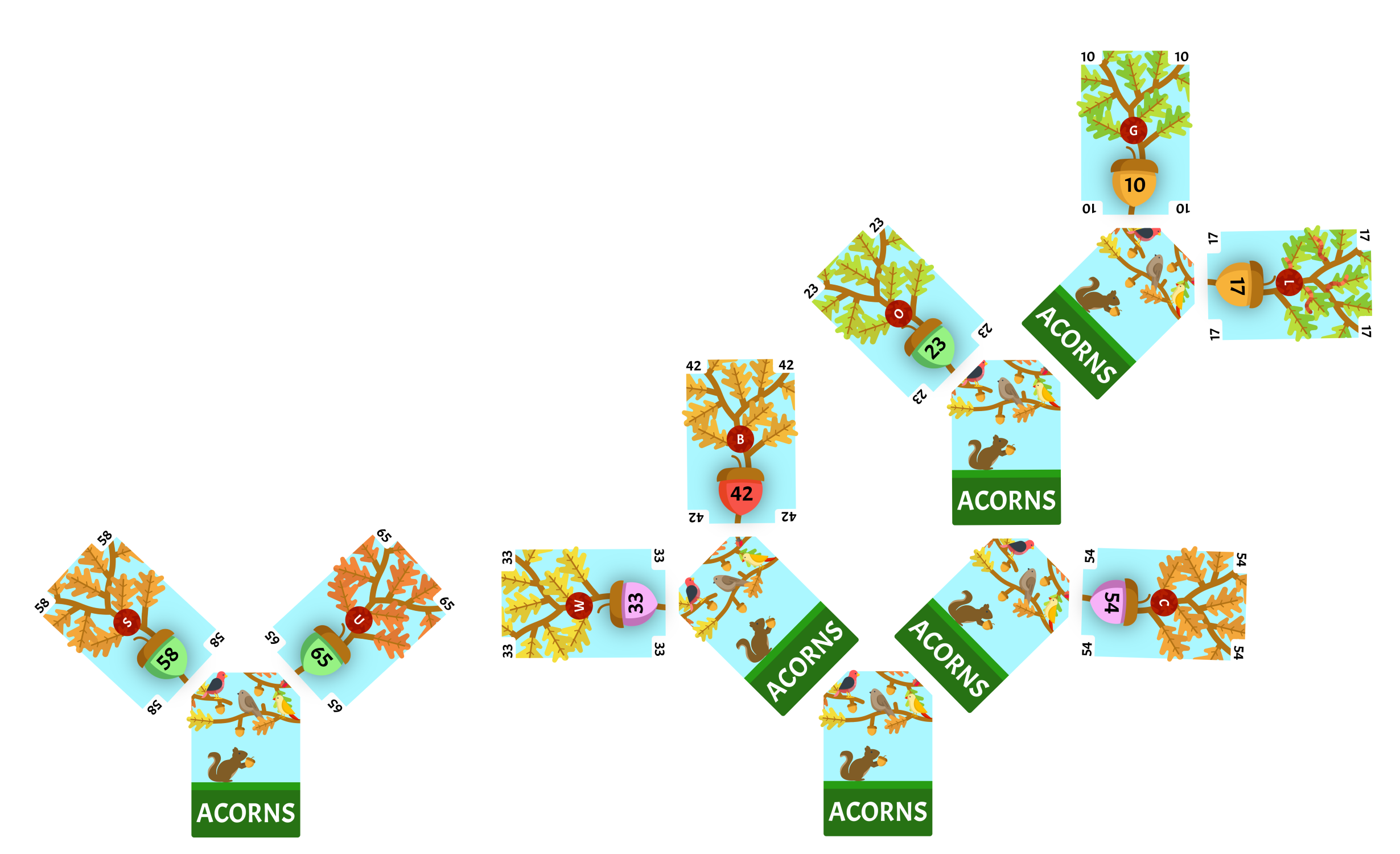
We will remove the two least-valued cards, our face-down card with a value of 123 and our face-down card with a value of 176 from our collection. We will draw a card from the deck and place it face-down as the root of a new subtree. 123 is the least-value of the two cards we removed so it will be the left child of the root card. 176 is the greatest-value of the two cards we removed so it will be the right child of the root card. The value of the face-down card is 299, we will reinsert it into the collection with all of it’s children intact and sort the collection. There is only 1 card in the collection, so we are finished.
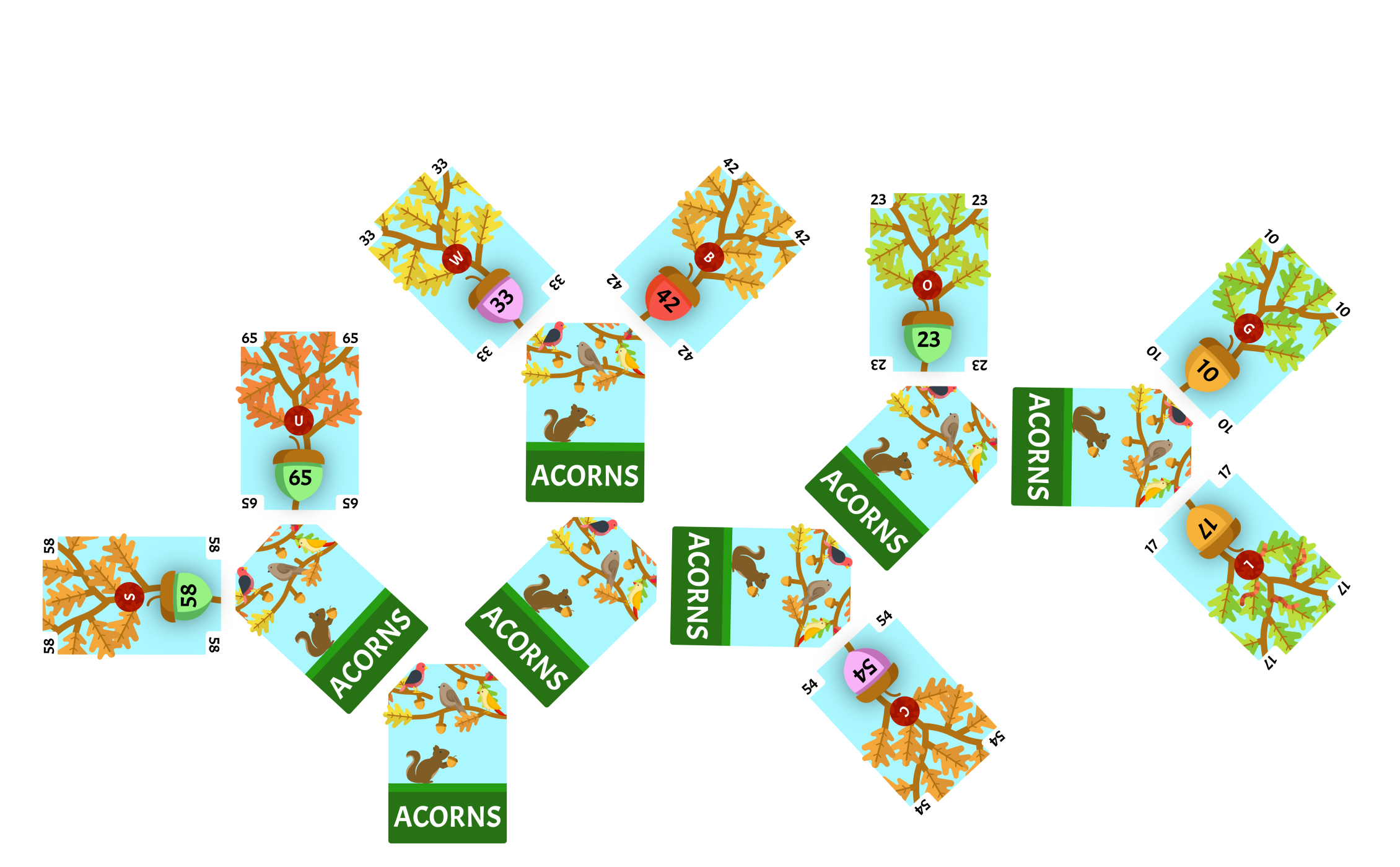
Assigning a Binary Value
Assign O
We start at the root card of the tree as our current card. The leaf corresponding to the chit O is 23.
The next card in the path to 23 is the right child of the current card, so the next binary number is 1. The right child is the new current card. Our current binary value for 23 is 1.
The next card in the path to 23 is the right child of the current card, so the next binary number is 1. The right child is the new current card. Our current binary value for 23 is 11.
The next card in the path to 23 is the left child of the current card, so the next binary number is 0. The left child is the new current card. Our current binary value for 23 is 110.
The next card in the path to 23 is the left child of the current card, so the next binary number is 0. The left child is the new current card. Our current binary value for 23 is 1100.
The current card is 23 which is the leaf corresponding to the chit we are looking to assign, so we are finished. The binary value for O is 1100.