Heap Removal Algorithm
Goals
Students will understand elements of the removal algorithm for heaps.
Video
Materials
One deck of Acorn cards.

Setup
Shuffle the deck and deal each student 9 cards.
Each student will shuffle their 9 cards, and then create a heap as demonstrated on the insertion algorithm page.
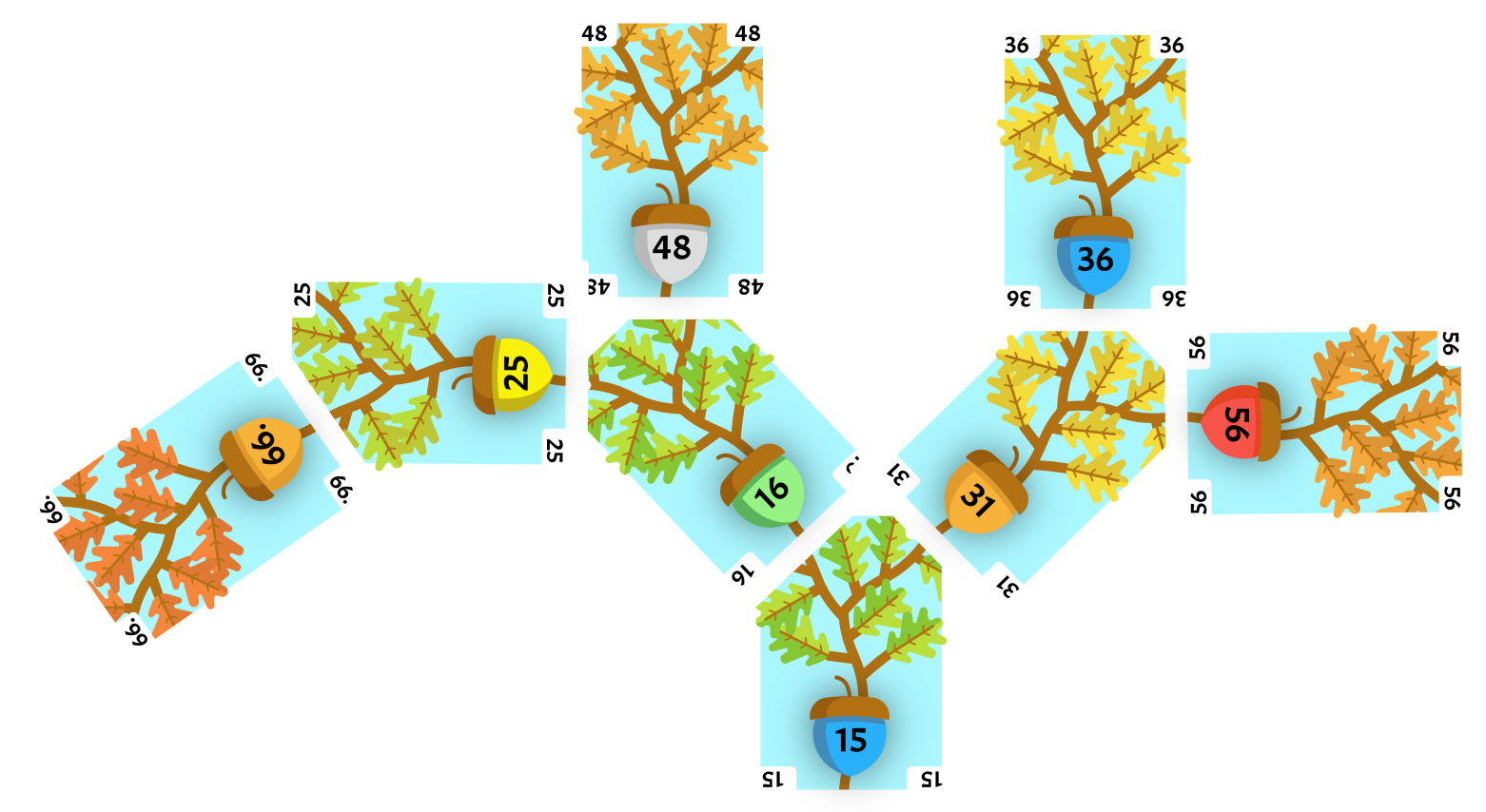
Algorithm
This algorithm will remove smallest card in the heap, which is at the root, while maintaining the heap property that every parent is smaller than its children.
Find the cards with level equal to the height of the tree. These will be the furthest away from the root of the tree. Find the right-most of these cards, which we will call the selected card.
Swap the selected with the root card.
Now, repeat the Swap If Higher section below for as long as needed to find the correct location for the selected card in the heap.
Once this is complete, you can remove the card which used to be the root.
Swap If Higher
Once the selected card has swapped with the root card, repeat the step below until you have found the final location of the selected card in the tree.
- If the selected card is a leaf, then stop.
- If the selected card is greater than any of its child cards and the smallest child is not the old root card, swap the selected card with the smallest child card and repeat the Swap If Higher steps. Otherwise, swap the selected card with the smallest child card that is not the old root card and repeat the Swap If Higher steps.
Example
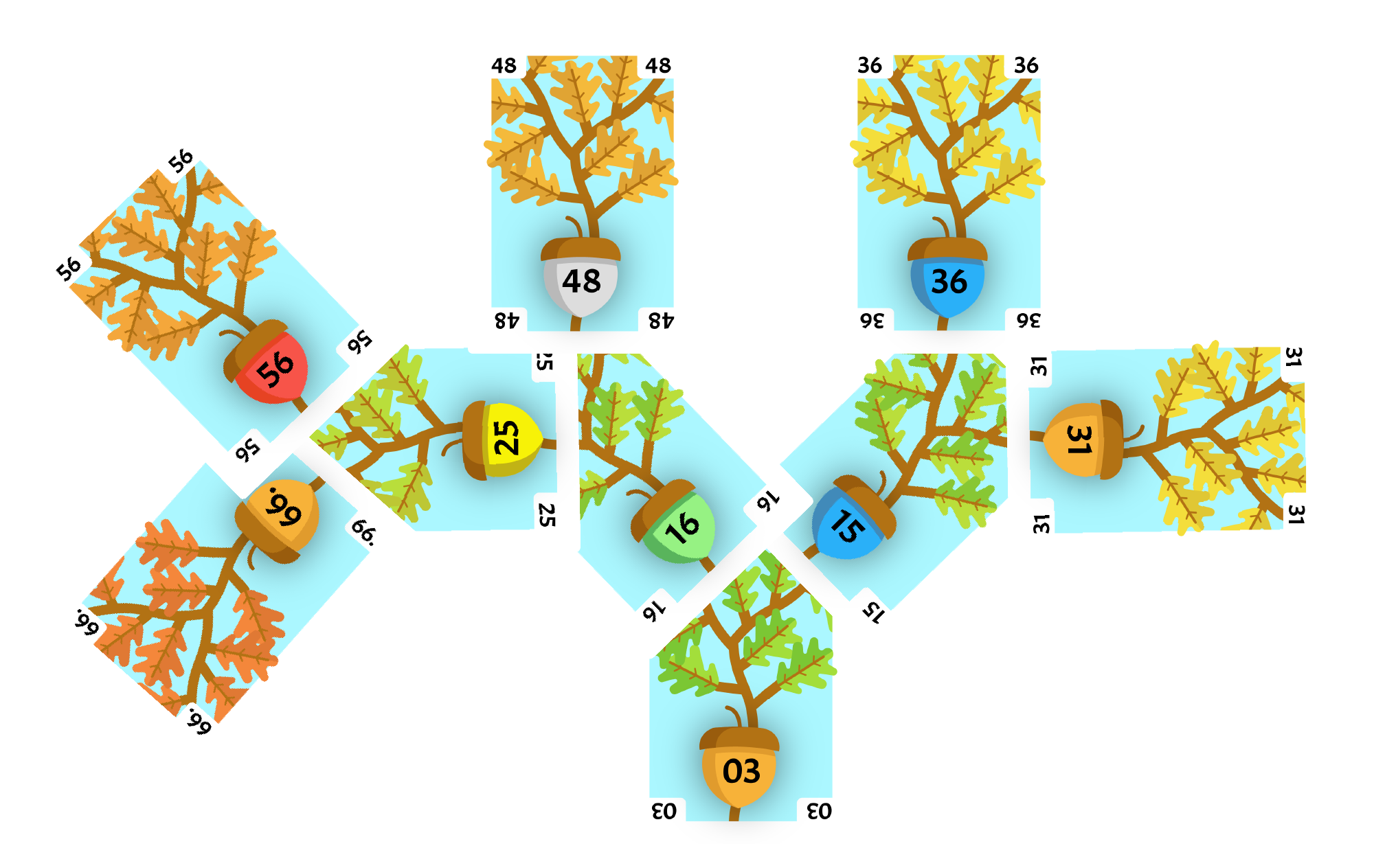
56 is the right-most card of the highest level of the tree, so it will be our selected card. It is swapped with the root card of the tree 03.
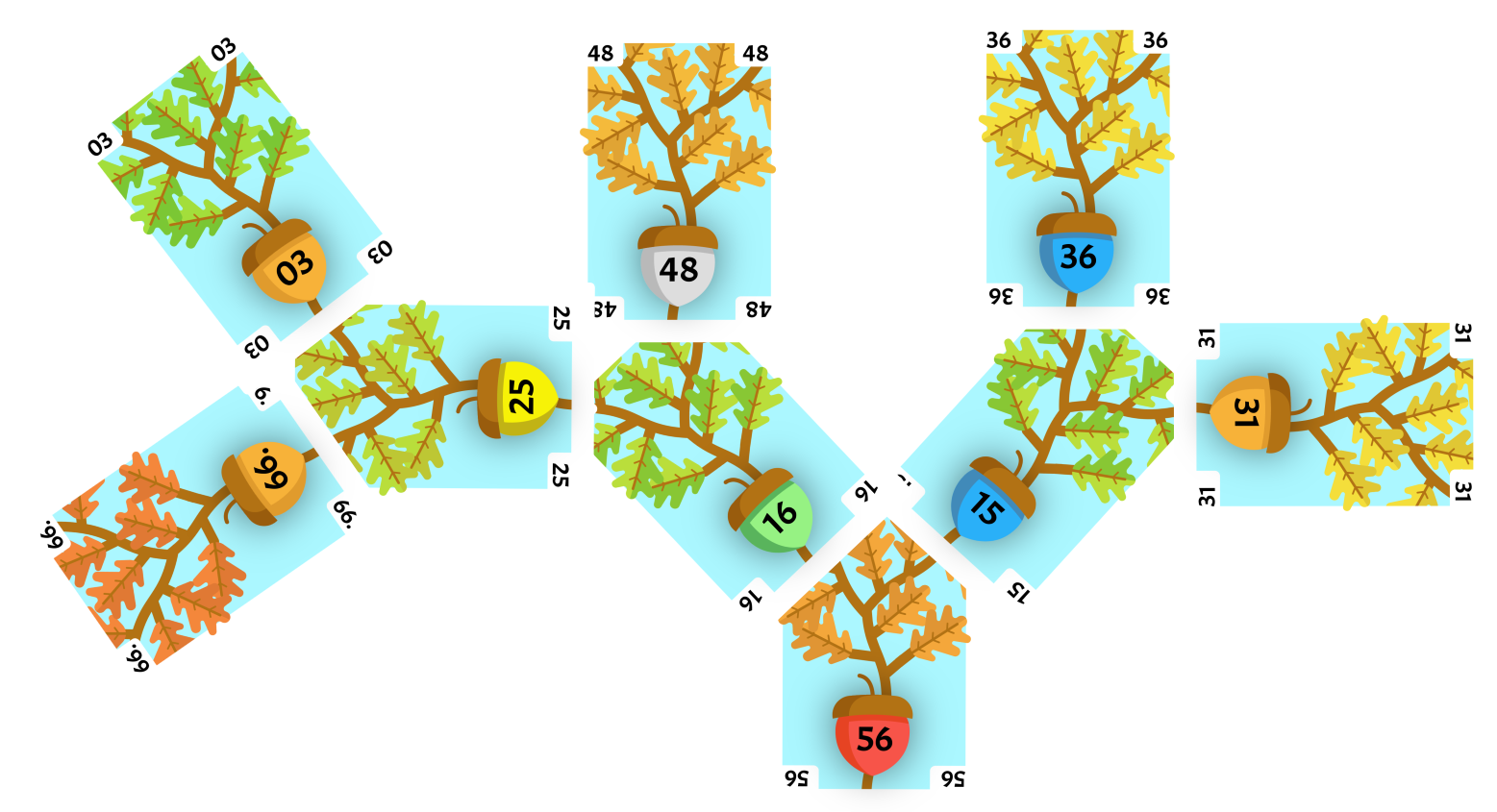
56 is greater than both of its children, so we must swap. 15 is the smallest child of 56 so we swap that one.
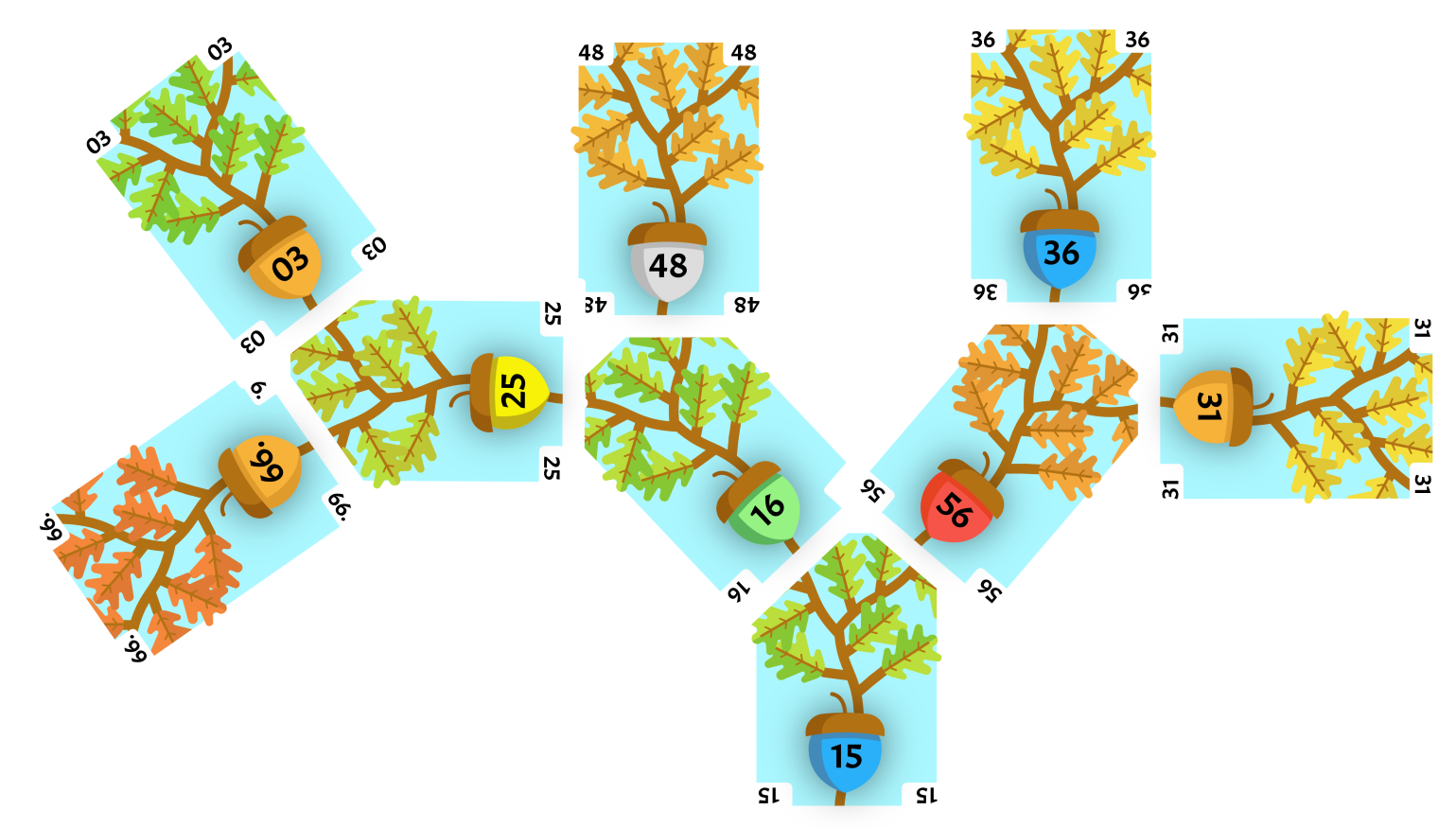
56 is greater than both of its children, so we must swap. 31 is the smallest child of 56 so we swap that one.
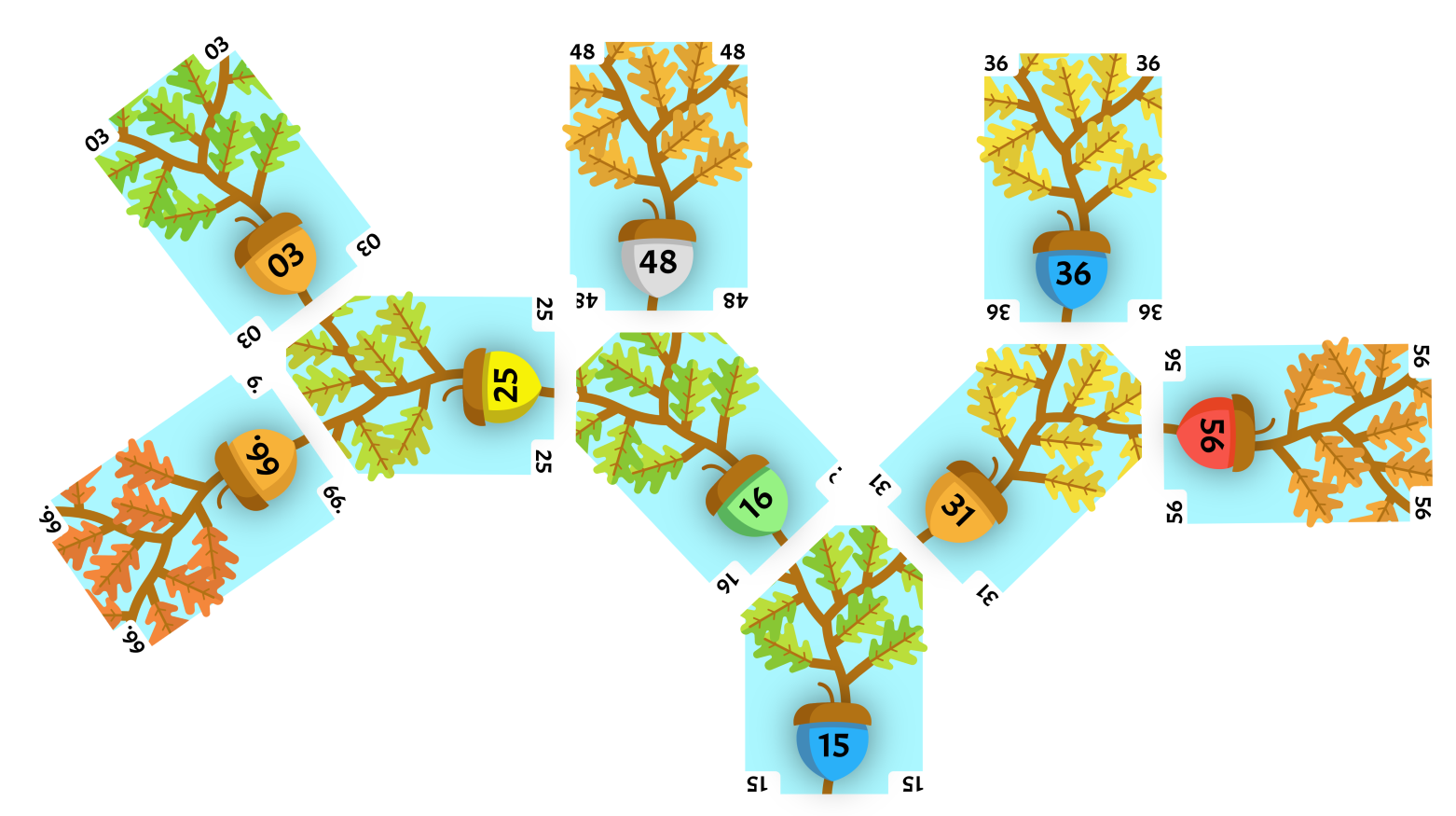
56 is now a leaf, so we stop. 03 used to be our root, so now it can be removed.